Singulär punkt
Från Rilpedia

Plot (färg representerar argument, ljusstyrka absolutbelopp) av exp(1 / z) med en väsentlig singularitet i origo
Singulär punkt, singuläritet är ett begrepp inom komplex analys. En singulär punkt är en punkt där en för övrigt analytisk funktion f ej är definierad. Man skiljer på tre olika sorters singulariteter: Låt f vara analytisk i en omgivning av z0, undantaget z0.
- Hävbar singularitet: z0 säges vara en hävbar singularitet till f om f kan omdefinieras i z0 och på så vis ge en funktion analytisk i en omgivning av z0 (medtaget z0).
- Pol: En punkt z0 säges vara en pol till f om
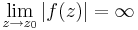 .
. - Väsentlig singularitet: En punkt z0 säges vara en väsentlig singularitet till f om f(z0) ej är definierad och z0 varken är en hävbar singularitet eller en pol.



