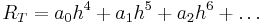Runge-Kuttametoden

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Runge-Kuttametoden approximerar högre ordningens derivator med hjälp av funktionsevalueringar.

Kan jämföras med en mer sofistikerad Eulers stegmetod.

Beskrivning

Metoden definierar en följd 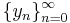\{y_n \}_{n=0} ^\infty rekursivt där yi approximerar den exakta lösningen y till differentialekvationen 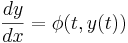\frac{dy}{dx} = \phi(t, y(t)) i punkten 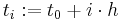t_i := t_0 + i \cdot h, där steglängden h och startpunkten (t0,y0) är given.

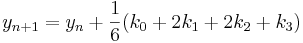y_{n+1} = y_n + \frac{1}{6}(k_0 + 2k_1 + 2k_2 + k_3),

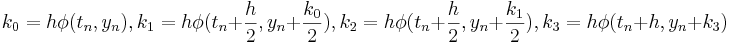k_0 = h \phi(t_n, y_n), k_1 = h \phi(t_n + \frac{h}{2}, y_n + \frac{k_0}{2}), k_2 = h \phi(t_n + \frac{h}{2}, y_n + \frac{k_1}{2}), k_3 = h \phi(t_n + h, y_n + k_3) . För trunkeringsfelet gäller

R_T = a_0h^4 +a_1h^5 +a_2h^6 + \ldots


Lebesgue Icon.svg Denna artikel om matematisk analys är bara påbörjad. Du kan hjälpa till genom att utöka den.
Hämtad från "https://sv.rilpedia.org/wiki/Runge-Kuttametoden"
Personliga verktyg