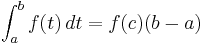Medelvärdessatsen

Från Rilpedia

Texten från svenska Wikipedia

Den sats som brukar kallas medelvärdessatsen är differentialkalkylens medelvärdessats. Men det finns också en sats som kallas integralkalkylens medelvärdessats.

Differentialkalkylens medelvärdessats

Om en funktion f(x) är kontinuerlig på det slutna intervallet [a,b] och deriverbar på det öppna intervallet (a,b), så finns en punkt ξ i (a,b) sådan att

$f(b) -f(a)=f'(\xi)(b-a)\,$ .

Bevis

Inför hjälpfunktionen

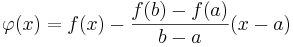$\varphi(x)=f(x)-\frac{f(b)-f(a)}{b-a}(x-a)$ .

Insättning av x = a och x = b ger φ(a) = φ(b) = f(a). Vidare är φ kontinuerlig i [a,b] och deriverbar i (a,b) med

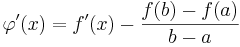$\varphi '(x)= f'(x)-\frac{f(b)-f(a)}{b-a}$ .

Rolles sats ger nu att φ har en stationär punkt, x = ξ, i intervallet (a,b), och i en sådan gäller att

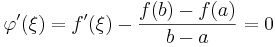$\varphi '( \xi )=f'(\xi )-\frac{ f(b)-f(a)}{b-a}=0$ ,

vilket bara är en omskrivning av det vi är ute efter. Q.E.D.

Satsen är ett specialfall av Taylors formel. Satsen kan även generaliseras till den generaliserade medelvärdessatsen (eller Cauchys medelvärdessats) som säger att:

Om funktionerna f och g är kontinuerliga på [a,b] och deriverbara på (a,b), så finns en punkt ξ i (a,b) sådan att

$g'(\xi)\bigl[f(b)-f(a)\bigr] = f'(\xi)\bigl[g(b)-g(a)\bigr]$ .

Differentialkalkylens medelvärdessats är då specialfallet g(x) = x.

Integralkalkylens medelvärdessats

Om f är en kontinuerlig funktion på det slutna intervallet [a,b], så finns en punkt c i (a,b) sådan att

$\int_a^b f(t) \, dt = f(c) (b - a)$

Värdet f(c) i satsen är funktionens medelvärde på intervallet.

Bevis

Eftersom f är kontinuerlig på [a,b] så antar f ett största värde M och ett minsta värde m, enligt max-min-satsen. Speciellt har vi alltså 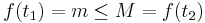$f(t_{1})=m \le M=f(t_{2})$ på intervallet [a,b]. Då gäller

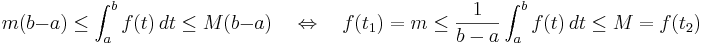$m(b-a) \le \int_{a}^{b} f(t)\, dt \le M(b-a)\quad\Leftrightarrow\quad f(t_{1})=m \le \frac{1}{b-a} \int_{a}^{b} f(t)\, dt \le M=f(t_{2})$ .

Enligt satsen om mellanliggande värden så finns c mellan $t 1$ och $t 2$ så att 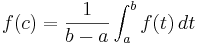$f(c)=\frac{1}{b-a}\int_{a}^{b} f(t)\, dt$ .

Medelvärdessatsen

Från Rilpedia

Differentialkalkylens medelvärdessats

Integralkalkylens medelvärdessats

Visningar

Personliga verktyg

Sök

Navigering

Bibeln

Övrigt

Verktygslåda

På andra språk