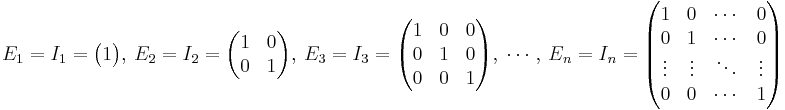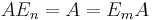Enhetsmatris

Från Rilpedia

Version från den 9 december 2008 kl. 19.10 av TXiKiBoT (Diskussion)
(skillnad) ← Äldre version | Nuvarande version (skillnad) | Nyare version → (skillnad)
Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

I linjär algebra är en enhetsmatris eller identitetsmatris med storleken n den kvadratiska n-gånger-n-matris som har ettor längs huvuddiagonalen (från övre vänstra till nedre högra hörnet) och nollor överallt annars. Den betecknas En, eller bara E om storleken är betydelselös eller kan avgöras av sammanhanget. Även In respektive I används ibland som beteckning.

E_1 = I_1 = \begin{pmatrix} 1 \end{pmatrix} ,\ E_2 = I_2 = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} ,\ E_3 = I_3 = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} ,\ \cdots ,\ E_n = I_n = \begin{pmatrix} 1 & 0 & \cdots & 0 \\ 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 1 \end{pmatrix}

En viktig egenskap för enhetsmatriser är att

AE_n = A = E_mA\,

för varje 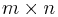m\times n-matris A. Enhetsmatrisen är också sin egen invers. Den i:te kolonnen i en enhetsmatris är enhetsvektorn ei. Enhetsvektorerna utgör också en bas för enhetsmatrisens enda egenrum, som svarar mot egenvärdet 1, som sålunda är det enda egenvärdet, med multiplicitet n. Med andra ord är samtliga nollskilda vektorer egenvektorer med egenvärdet 1. Av detta följer att identitetsmatrisens determinant är 1.

När n-gånger-n-matriser används för att beskriva linjära transformationer från ett n-dimensionellt vektorrum till sig självt, står En för identitetsfunktionen, oavsett vilka basvektorer som används.

Källor

Artikeln är, helt eller delvis, en översättning från en annan språkversion av Wikipedia.
Hämtad från "https://sv.rilpedia.org/wiki/Enhetsmatris"
Personliga verktyg