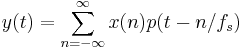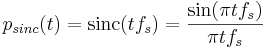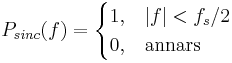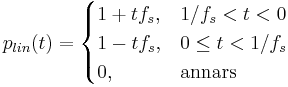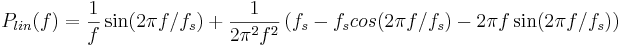Pulsamplitudmodulering

Från Rilpedia

Version från den 6 januari 2007 kl. 09.47 av Hejkompis (Diskussion)

(skillnad) ← Äldre version | Nuvarande version (skillnad) | Nyare version → (skillnad)

Hoppa till: navigering, sök

Texten från svenska Wikipedia

Pulsamplitudmodulering, PAM (engelska: Pulse-Amplitude Modulation), är en linjär metod för att interpolera vid konvertering av en tidsdiskret funktion eller en sekvens till en tidskontinuerlig funktion. Det används bland annat för att rekonstruera samplat material.

Pulsamplitudmodulering av en tidsdirekt funktion $x (n)$ samplad med samplingsfrekvensen $f s$ till en tidskontinuerlig funktion $y (t)$ med pulsfunktionen $p (t)$ kan skrivas som:

$y(t) = \sum_{n=-\infty}^{\infty} x(n) p(t-n/f_s)$

Pulsfunktionen $p (t)$ bestämmer hur frekvensåtergivningen blir.

Y (f) = X (f / f s) P (f)

Notera att Fourier-transformen av en tidsdiskret funktion är periodisk. Den pulsamplitudmodulerade funktionen kan alltså innehålla frekvenser som ligger utanför det område som den tidsdiskreta representerar.

Perfekt rekonstruktion, givet att det samplade materialet var perfekt bandbegränsat i intervallet $[ - f s / 2, f s / 2]$ , fås med hjälp av sinc-funktionen:

$p_{sinc}(t) = \mbox{sinc}(t f_s) = \frac{\sin(\pi t f_s)}{\pi t f_s}$