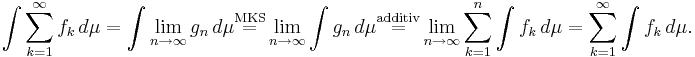Beppo Levis sats

Från Rilpedia

Version från den 9 maj 2009 kl. 07.54 av Petter Strandmark (Diskussion)
(skillnad) ← Äldre version | Nuvarande version (skillnad) | Nyare version → (skillnad)
Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Beppo Levis sats är en matematisk sats i måtteori. Den säger att måttintegralen är sigma-additiv med avseende på icke-negativa mätbara funktioner. Satsen är uppkallad efter den italienska matematikern Beppo Levi som bevisade den. Observera att det finns andra satser som kallas Levis sats.

Satsen

Låt 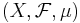(X,\mathcal{F},\mu) vara ett måttrum och 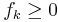f_k \geq 0 vara mätbara funktioner. Beppo Levis sats säger att

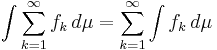\int \sum_{k=1}^\infty f_k\,d\mu = \sum_{k=1}^\infty \int f_k\,d\mu .

Bevis

Detta är en enkel följd av monotona konvergenssatsen, som kan appliceras på alla delsummor av de oändliga summorna:

För 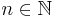n \in \N, betecka

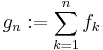g_n := \sum_{k=1}^n f_k.

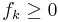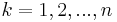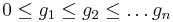Eftersom f_k \geq 0\, för alla k = 1,2,...,n\, så är 0 \leq g_1 \leq g_2 \leq \ldots g_n mätbara funktioner. Därför är monotona konvergenssatsen möjlig att använda för funktionerna 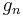g_n\,. Eftersom måttintegralen är additiv så är

\int \sum_{k=1}^\infty f_k\,d\mu = \int \lim_{n \rightarrow \infty} g_n\,d\mu \stackrel{\mathrm{MKS}}{=} \lim_{n \rightarrow \infty} \int g_n\,d\mu \stackrel{\mathrm{additiv}}{=} \lim_{n \rightarrow \infty} \sum_{k=1}^n \int f_k\,d\mu = \sum_{k=1}^\infty \int f_k\,d\mu .

Vilket bevisar satsen.

Se även

Hämtad från "https://sv.rilpedia.org/wiki/Beppo_Levis_sats"
Personliga verktyg