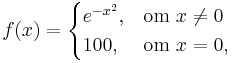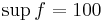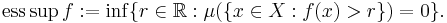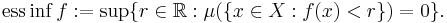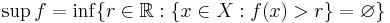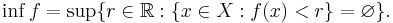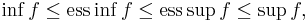Väsentligt supremum och väsentligt infimum
Från Rilpedia
Väsentligt supremum och väsentligt infimum är idéer inom matematik som förenar supremum och infimum med måtteori.
Innehåll |
Bakgrund
Skillnaden mellan vanligt supremum och väsentligt supremum är att nollmängder inte påverkar det väsentliga supremumet. Till exempel, om funktionen 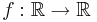 är definierad som
är definierad som
så är
men för alla 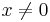
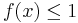 .
.
Det vill säga att det finns bara en punkt där 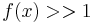 . Därför kan man säga att det är inte "resonligt" att supremumet för f är 100. Man får ingen informationen från talet 100.
. Därför kan man säga att det är inte "resonligt" att supremumet för f är 100. Man får ingen informationen från talet 100. 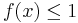 nästan överallt i
nästan överallt i 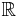 , så att det "väsentliga" supremumet för f borde vara 1. Så man definierar väsentliga supremumet för f till 1. På likartat sätt definieras väsentligt infimum.
, så att det "väsentliga" supremumet för f borde vara 1. Så man definierar väsentliga supremumet för f till 1. På likartat sätt definieras väsentligt infimum.
Formell definition
Låt 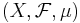 vara ett måttrum och en mätbar funktion
vara ett måttrum och en mätbar funktion 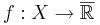 .
.
Väsentligt supremum för f är det minsta reella tal r så att mängden av alla x i X som uppfyller f(x) > r är en nollmängd:
Väsentligt infimum för f är det största reella tal r så att mängden av alla x i X som uppfyller f(x) < r är en nollmängd:
Beteckningen "ess" kommer från engelskans "essential" ("väsentlig").
Koppling till vanligt supremum och infimum
Detta kan jämföras med vanligt supremum och infimum. Det går att visa att supremum för mätbara funktionen 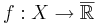 är det minsta reella tal r så att mängden av x i X som uppfyller
är det minsta reella tal r så att mängden av x i X som uppfyller 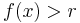 är tom:
är tom:
och infimum för f är det största reella tal r så att mängden av x i X som uppfyller 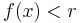 är tom:
är tom:
Därför
eftersom 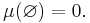
Tillämpningar
Väsentligt supremum har många tillämpningar inom måtteori och funktionalanalys.
Norm
- Huvudartikel: Supremumnormen.
Med väsentligt supremum kan man definiera en norm som kallas väsentlig supremumnorm.
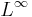 -rum
-rum
- Huvudartikel: Lp-rum.
Med väsentliga supremumnormen kan man definiera begreppet väsentligt begränsad funktion, dvs rummet 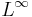 .
.