LP-problem

Från Rilpedia

Texten från svenska Wikipedia

LP-problem; Linjärprogrammeringsproblem är en typ av optimeringsproblem med den egenskapen att målfunktionen och samtliga bivillkor är linjära funktioner. LP-problemen betraktas inom optimeringsläran som förhållandevis lätta även om de i praktiska tillämpningar endast i sällsynta fall kan lösas utan datorstöd (då t.ex med hjälp av simplexmetoden)

Det generella LP-problemet kan skrivas som:

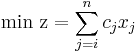
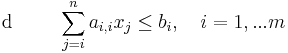
Där z är målfunktionen som skall optimeras, variablerna x_j är de n-stycken beslut som ska fattas, c_j är kostnaderna för besluten och x₍i,j) och x_i definerar de m-stycken bivillkor (krav) som måste vara uppfyllda.

Standardform

Standardformen för ett LP-problem är en omskrivning av problemet så att samtliga variabler är ickenegativa samt att samtliga bivillkor formulerats som likhetsvillkor. Det sistnämnda kan uppnås genom att icke-negativa slackvariabler introduceras i samtliga olikhetsvillkor där slackvariabeln utjämnar likheten.

Exempelvis kan olikheten:

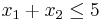
Skrivas som:

x₁ + x₂ + a₁ = 5

Där a₁ är en ickenegativ slackvariabel som kan betraktas som kvarvarande frihet.

icke-negativitet för alla variabler uppnås genom variabelbyte då varibler ersätts med y₁ = − x₁ och fria varibler delas i två variabler. dvs x₁ = y₁ − y₂ där y₁ kommer vara noll när och y₂ kommer vara noll när 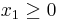. Båda de nya variablerna är dock ickenegativa emedans x₁ var fri.

Omskrivning på standardform innebär inte sällan att antalet variabler ökar betydligt vilket givetvis kan försvåra beräkningarna men då LP-problem i praktisk sammanhang nästan uteslutande löses med datorstöd är detta ett litet pris att betala för att kunna använda generella algoritmer som t.ex simplexmetoden.

Baslösning

Baslösningar är ett sätt att vid lösningen av LP-problem beskriva extremlösningar (hörnpunkter i definitionsmängden). Baslösningar används bl.a. av simplexmetoden för att systematiskt avsöka extrempunkterna.

För ett LP-problem skrivit på standardform kan alla lösningar tecknas som en vektor av problemets samtliga variabler (även slackvariabler).

Ur ett ekvationssytem (här på matrisform A är en n*m-matris) Ax = b erhålles en baslösning om n-m variabler sätts till 0 och det kvarvande ekvationssystemet löses.

Här kallas de variabler som löses ut för basvariabler och då de entydigt bestämmer hörnpunkten, övriga variabler (som är noll) kalls icke-basvariabler eller ibland nollvariabler.

Speciellt är en baslösning där alla element i vektorn är icke-negativa en tillåten baslösning dvs den uppfyller bivillkoren för LP-problemet.

En baslösning är degenererad om någon av basvariablerna beräknats till noll dvs om andra variabler kunde väljas som icke-basvariabler och ändå generera samma hörnpunkt.

Egenskaper

Det tillåtna området (de punkter: (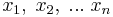) som satsiferar samtliga bivillkor) till ett LP-problem kommer alltid vara en konvex mängd. Denna egenskap följer direkt av att bivillkoren är linjära.

Denna egenskap tillsammans med målfunktionens liniarietmmedför att lokala optima även är globala och leder fram till Linjärprogrammeringens fundamentalsats.