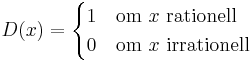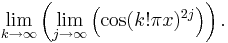Dirichlets funktion
Från Rilpedia
Version från den 27 oktober 2008 kl. 20.38 av Calle (Diskussion)
Dirichlets funktion är inom matematisk analys en funktion på de reella talen som inte är kontinuerlig någonstans, uppkallad efter den tyske matematikern Dirichlet. Definitionen är
Funktionen kan dock konstrueras som ett gränsvärde av kontinuerliga funktioner:
Dirichlets funktion är Lebesgueintegrerbar, men inte Riemannintegrerbar.