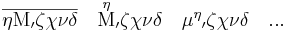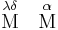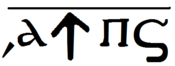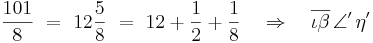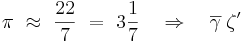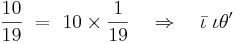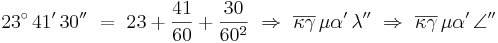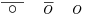Joniska talbeteckningssystemet
Från Rilpedia
| Grekiska alfabetet | |||||
|---|---|---|---|---|---|
| Enhetsalfabetet | |||||
| Α α Alfa | Ν ν Ny | ||||
| Β β Beta | Ξ ξ Xi | ||||
| Γ γ Gamma | Ο ο Omikron | ||||
| Δ δ Delta | Π π Pi | ||||
| Ε ε Epsilon | Ρ ρ Rho | ||||
| Ζ ζ Zeta | Σ σ ς Sigma | ||||
| Η η Eta | Τ τ Tau | ||||
| Θ θ Theta | Υ υ Ypsilon | ||||
| Ι ι Jota | Φ φ Phi | ||||
| Κ κ Kappa | Χ χ Chi | ||||
| Λ λ Lambda | Ψ ψ Psi | ||||
| Μ μ My | Ω ω Omega | ||||
| Extra tecken i äldre alfabet1 | |||||
|
|
|||||
| 1 Källa: Nationalencyklopedin | |||||
Det joniska talbeteckningssystemet har använts i Grekland sedan 500-talet f.Kr. och är fortfarande i bruk, även om det främst används för ordningstal. Det är baserat på det grekiska alfabetet.
Innehåll |
Historia
Under 500-talet f.Kr. utvecklades vetenskapen generellt i grekiska Jonien. De joniska städerna var i förbund med Lydien, som nådde sin höjdpunkt under Krösus. När Lydien invaderades av perserna 547 f.Kr fick grekerna i Jonien även kontakt med babylonisk matematik. I regionen uppstod då en mer modern form av vetenskap, som krävde bevis istället för att bara fungera. Flera tidiga vetenskapsmän levde här, bland annat Thales från Miletos. Samtidigt utvecklades här även ett nytt talbeteckningssystem.
Trots att systemet skapades på 500-talet, tog det tid innan det kom i allmänt bruk i den hellenistiska världen. Först på 300-talet f.Kr präglades mynt som använde systemet. Därefter tog det ytterligare ungefär 100 år innan det blev dominerande.
Endast majuskelskrift användes fram till 300-talet e.Kr. Därefter utvecklades skriften till uncialskrift och sedermera minuskelskrift. Vissa bokstäver förändrades mer än andra, kanske allra mest de rent numeriska tecknen koppa och sampi. När uncialskriften användes, förväxlades dessutom digamma med ligaturen stigma; bokstavsformerna var förvillande lika. Därför ser det moderna joniska talbeteckningssystemet något annorlunda ut än det ursprungliga.
Struktur
Talbeteckningssytemet använde de 24 bokstäver i det nuvarande grekiska alfabetet, samt tre äldre bokstäver för att beteckna tal. De första nio symbolerna fick då beteckna talen 1-9, nästa nio betecknade tiotalen 10-90 och de sista nio hundratalen 100-900. Ingen symbol för talet noll fanns. Talen bildades sedan additivt utifrån dessa symboler. De kunde skrivas antingen med det mest värda talet först eller sist, så ΣΛΓ och ΓΛΣ betydde båda 233. Den senare formen har dock varit ovanligare, historiskt sett, och är direkt fel i modern grekiska.
-
Joniska siffror 1 Α α Alfa 10 Ι ι Jota 100 Ρ ρ Rho 2 Β β Beta 20 Κ κ Kappa 200 Σ σ Sigma 3 Γ γ Gamma 30 Λ λ Lambda 300 Τ τ Tau 4 Δ δ Delta 40 Μ μ My 400 Υ υ Ypsilon 5 Ε ε Epsilon 50 Ν ν Ny 500 Φ φ Fi 6 Ϝ ϛ Digamma → Stigma 60 Ξ ξ Xi 600 Χ χ Chi 7 Ζ ζ Zeta 70 Ο ο Omikron 700 Ψ ψ Psi 8 Ε ε Eta 80 Π π Pi 800 Ω ω Omega 9 Θ θ Theta 90 Ϙ ϟ Koppa 900 Ϡ ϡ Sampi Klassiska siffror som versaler, moderna som gemener.
Tal över 999
Tyvärr räcker bara ovanstående 27 tecken till att skriva tal upp till 999. För att skriva tusental återanvändes siffrorna 1-9 (bokstäverna α till θ) med en apostrof före, antingen nertill eller upptill (idag är nertill standard). På detta sätt kunde man beteckna alla tal mellan 1 och 9 999 med endast maximalt fyra bokstäver.
Inte heller detta system räcker för att skriva större tal än så utan att bli tvetydigt. För 10 000 användes därför bokstaven M som var begynnelsebokstaven i det grekiska ordet myrioi eller myriades[1]. Mångfalder av 10 000 skrevs multiplikativt med multiplikatorn före, ovanför eller efter M. Under den klassiska epoken kunde exempelvis talet 21 234 567 skrivas ’BΡΚΓΜ’ΕΦΞΖ.
Talet 87 654 har alltså kunnat skrivas på en mängd olika sätt.
Multiplikatorn kunde även innehålla flera siffror, som 34 (λδ). Den skrevs även ut för ett, för att visa att det var en myriad, och inte talet 40.
I texter kunde dessutom ordet myriades skrivas ut direkt, som λδ’ μυριάδες.
Utmärkning av tal i text
Eftersom talen med det joniska talbeteckningssystemet använder samma tecken som omkringliggande texter, finns det ett behov av att markera vilka tecken som symboliserar numeriska värden. I princip har två system använts: en apostrof till höger om talet, eller en linje över talet. Under antiken och medeltiden användes främst en linje över talet (15 = ιε), idag är det standard med en apostrof till höger (κεραῖα, keraia; 15 = ιε’).
Rationella tal
Innan decimalsystemet slog igenom använde grekerna ett antal olika sätt för att ange reella tal. Alla hade det gemensamt att de endast hanterade rationella tal. Övriga tal avrundades.
Speciella tecken
Ett fåtal rationella tal hade speciella tecken. Det gällde framför allt 1/2 som skrevs ∠’. Ibland användes även ω’ för 2/3. Dessa tecken kunde kombineras med andra system.
Enhetsbråk
Den vanligaste formen för rationella tal var addition av enhetsbråk, ett system som hade använts tidigare bland annat i Egypten. Systemet går ut på att ett bråktal skrivs som en summa av andra bråktal. Täljaren i dessa antas vara 1 (ett), så endast nämnaren skrivs ut.
Exempel med 101 åttondelar respektive talet π (pi):
Bråk med annan täljare
I undantagsfall har det hänt att bråktalen har angetts med både täljare och nämnare. En riktigare syn är kanske att talen då skrevs som enhetsbråk med en multiplikator.
Sexagesimalt talsystem
Inom bland annat astronomin användes ett annat system, det sexagesimala talsystemet, som kom från babylonierna. Det innebar att bråkdelen av tal angavs som ett antal siffror med bas 60.
Ett exempel på hur Klaudios Ptolemaios kunde ange en vinkel i sin bok Almagest:
Nollan
I och med att de grekiska astronomerna övertog babyloniernas sexagesimala talsystem, så uppstod även ett behov av en nolla. Nollan hade använts några århundraden tidigare i kilskrift (äldsta fyndet från 300-talet f.kr.). Det är troligen denna som grekerna lånar in under 100-talet e.Kr.[2] Den används för att fylla ut delar av tal som saknas, exempelvis heltals- eller sekunddelen.
Den grekiska nollan ser ut som en liten cirkel med ett långt streck över. Efter hand blir cirkeln större, och strecket allt mindre. Utseendet går då mer och mer mot bokstaven omikron, eller den moderna nollan.
Siffror i modern grekiska
I modern grekiska används i stort sett bara arabiska siffror. Det joniska talbeteckningssystemet används ibland för ordningstal, ungefär som romerska siffror används i Sverige. Till exempel numreras kungar och divisioner i fotbollsligan på detta sätt. Även list- och kapitelnumrering kan ske med joniska siffror. Lagar numreras alltid på detta sätt.
Som regel används versaler i modern grekiska. Gemener kan användas exempelvis i listor, framför allt om det är listor som numreras i flera nivåer. Eftersom detta är vanligt, förstås åtminstone lägre tal allmänt.
Tal följs alltid av en apostrof (κεραῖα). Tusental markeras med en låg apostrof till vänsterom siffran. I modern grekiska förekommer så stora tal framför allt för årtal, så det är ovanligt att se andra bokstäver än alfa och beta i denna position.
Inom sentida typografi kan stigma (6) delas upp i sigma och tau. Bruket uppstod när typer saknades för stigma. Idag är stigma och sigma-tau digrafen helt utbytbara.
Siffror i Unicode
Unicode har haft stöd för det joniska talsystemet länge. Alla siffror ingår i samma block som det normala grekiska alfabetet, och det är vanligt att datorer stöder dem.
Se även
- Attiska talbeteckningssystemet
- Grekiska siffror
- Grekiska räkneord
- Grekiska alfabetet
- Romerska siffror
- Siffra
Referenser
Tryckta källor
- Haralambous, Yannis: From Unicode to Typography, a Case Study: the Greek Script, Boston mars 1999 (PDF) (engelska). Hämtat 29 juni 2008. Paper till 14th International Unicode Conference.
- Johansson, Bo Göran: Matematikens historia, Studentlitteratur, Lund 2004 (svenska). ISBN 91-44-03322-2.
- McLeish, John: Matematikens kulturhistoria, Bokförlaget Forum AB, 1991 (svenska). ISBN 91-37-10200-1.
- Mercier, Raymond: Proposal to encode the Greek Zero Sign in the UCS, 8 februari 2004 (PDF) (engelska). Hämtat 2 juli 2008.
- Thompson, Jan: Matematiken i historien, Studentlitteratur, Lund 1996 (svenska). ISBN 91-44-60081-X.
- The Unicode Consortium [1]: The Unicode Standard, Addison-Wesley Professional, [Oktober 1991] 3 november 2006 (PDF), version 5.0 (engelska). ISBN 0-321-48091-0. Hämtat 3 juli 2008.
- Verdan, Samuel: Systèmes numéraux en Grèce ancienne: description et mise en perspective historique, Institut d'archéologie et des sciences de l'Antiquité (IASA), Université de Lausanne, Lausanne 2007 (PDF) (franska). Hämtat 2 juli 2008.
Webbkällor
- Nicholas, Nick: Numerals, Thesaurus Linguae Graecae, University of California, Irvine 9 april 2005 (HTML) (engelska). Hämtat 2 juli 2008. [3]
- Nicholas, Nick: Non-Attic Letters, Thesaurus Linguae Graecae, University of California, Irvine 18 januari 2004 (HTML) (engelska). Hämtat 2 juli 2008. [3]
- O'Connor, J J; E F Robertson: Greek number systems, School of Mathematics and Statistics, University of St. Andrews, St. Andrews, Skottland januari 2001 (HTML) (engelska). Hämtat 2 juli 2008.
Fotnoter
- ↑ Myrios betyder ”oräknelig”. Härifrån har vi fått ordet myriad. ”Myra” heter för övrigt myrmos på grekiska.
- ↑ I annan litteratur, anges ofta nollan vara en förkortning av οὐδέν (intet), men detta förkastas i alla fall av Mercier (2004).
- ↑ 3,0 3,1 Källor finns på sidan: Nicholas, Nick: Greek Unicode Issues, Thesaurus Linguae Graecae, University of California, Irvine 29 juli 2006 (HTML) (engelska). Hämtat 2 juli 2008.