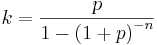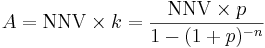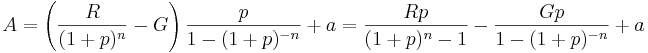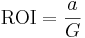Annuitetsmetoden

Från Rilpedia

Version från den 28 mars 2009 kl. 14.32 av Koios (Diskussion)
(skillnad) ← Äldre version | Nuvarande version (skillnad) | Nyare version → (skillnad)
Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Denna artikel handlar om metoden för investeringskalkylering. För låneformen, se annuitetslån.

Fördelningen av grundinvestering och restvärde över investeringens ekonomiska livslängd.

Annuitetsmetoden är en metod för investeringskalkyl. Den är nära kopplad till nuvärdemetoden. Metoden anger hur lönsam en investering är utslaget på investeringens livstid. Det erhållna värdet, annuiteten, anges som regel i kronor per år. Metoden är fördelaktig exempelvis om det ska fattas beslut om att köpa eller leasa en maskin eller dylikt, då resultatet blir direkt jämförbart med kostnaden för leasing. Den är även fördelaktig om investeringsalternativ med olika lång ekonomisk livslängd ska jämföras, eftersom det är resultat per år som erhålls.

Innehåll

 Beräkningar

Om nettonuvärdet redan är beräknat, kan detta enkelt fördelas över investeringens ekonomiska livslängd. Det multipliceras då helt enkelt med annuitetsfaktorn.

  • p = kalkylränta
  • k = annuitetsfaktor
  • A = annuitet
  • NNV = nettonuvärde
  • n = ekonomisk livslängd
k = { p \over { 1 - \left ( 1 + p \right )^{-n} } }
A = \mathrm{NNV} \times k = { { \mathrm{NNV} \times p } \over { 1 - (1 + p)^{-n} } }

Ska annuiteten beräknas direkt för en investering som har jämnt fördelade årliga inbetalningsöverskott, fördelas helt enkelt investeringskostnaden och nuvärdet av restvärdet (värdet då investeringens ekonomiska livslängd upphör) över tiden.

  • a = årligt inbetalningsöverskott (inbetalningar - utbetalningar)
  • G = grundinvestering
  • R = restvärde
A = \left ( { R \over { (1 + p)^n } } - G \right ) { p \over { 1 - (1+p)^{-n} } } + a = { { R p } \over { (1+p)^n - 1 } } - { { G p } \over { 1 - (1+p)^{-n} } } + a

Om betalningsströmmarna är ojämna över investeringens ekonomiska livslängd, fungerar tyvärr inte den sistnämnda metoden. Då måste nuvärdet (alternativt slutvärdet) beräknas först, för att därefter fördelas med den första metoden ovan.

Annuitetskvot

Annuitetskvoten, även kallad ROI efter engelskans Return on Investment, är annuiteten delat med grundinvesteringen. Den kan fylla samma funktion som kapitalvärdekvoten, vid investeringar med olika livslängd. Det innebär i stort sett att den bara fyller en funktion vid jämförelser av investeringar av olika storlek och livslängd, och endast när kapitalknapphet råder. Den indikerar även investeringens räntabilitet.

I sin enklaste form kan den beräknas som:

\mbox{ROI} = { a \over G }

För kortsiktiga investeringar, maximalt cirka ett år, kan helt enkelt summan av inbetalningsöverskotten delas med grundinvesteringen.

Referenser

Tryckta Källor

  • Nurmis, Peter; Ogi Chun: Övningskompendium, Kalkylering & rationalitet, Stockholms Universitet/Reproenheten, Stockholm [1994] 1997 "Formler",, 3:e uppl. (svenska). 
  • Andersson, Göran: Kalkyler som beslutsunderlag, Studentlitteratur, Lund [1983] 2001, 5:e uppl. (svenska). ISBN 91-44-01910-6. 

Webbkällor

Se även

 Externa Länkar

Hämtad från "https://sv.rilpedia.org/wiki/Annuitetsmetoden"
Personliga verktyg
På andra språk