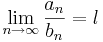Stolz-Cesàros sats

Från Rilpedia

Version från den 4 februari 2009 kl. 11.39 av Chobot (Diskussion)
(skillnad) ← Äldre version | Nuvarande version (skillnad) | Nyare version → (skillnad)
Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Stolz-Cesàros sats är ett resultat inom matematisk analys som kan användas för att avgöra huruvida en serie är konvergent.

Formulering

Låt (an) och (bn) vara två följder av reella tal. Antag att (bn) är strikt växande och obegränsad, samt att gränsvärdet

\lim_{n \to \infty} \frac{a_{n+1}-a_n}{b_{n+1}-b_n}=l existerar

Då gäller

\lim_{n\to\infty} \frac{a_n}{b_n} = l
Hämtad från "https://sv.rilpedia.org/wiki/Stolz-Ces%C3%A0ros_sats"
Personliga verktyg