Harmoniskt medelvärde
Från Rilpedia
Harmoniskt medelvärde är en typ av medelvärde.Harmoniskt medelvärde är inversen av reciprokernas aritmetiska medelvärde.Det harmoniska medelvärdet används främst till att beskriva tillväxtfenomen och i specialfall inom indexkalkyl. Harmoniska medelvärde används dock sällan då det aritmetiska medelvärdet beskriver likadana situationer lika bra. Det harmoniska medelvärdet är inte robust. Fastän det harmoniska medelvärdet räknas med hjälp av det aritmetiska medelvärdet beter de sig inte lika vid förlängning. För N stycken tal a1,..., aN är det harmoniska medelvärdet
![\bar{a}_H = {N \over {{1 \over a_1}+...+{1 \over a_N}}} = N\left[ \sum_{i=1}^n{a_i^{-1}} \right]^{-1}.](/w/images/sv.rilpedia.org/math/a/e/8/ae89da0693e22f0c42e8642d465e2884.png)
Innehåll |
Relationen till andra medeltal
Det harmoniska medelvärdet är ett av de tre Pythagoras medelvärdena.De två andra är aritmetiskt medelvärde och geometriskt medelvärde. Det harmoniska medelvärdet är alltid det minsta medelvärdet , det aritmetiska det störta och geometriska medelvärdet där i mellan.

Harmoniskt medelvärde inom andra vetenskap
Harmoniskt medelvärde används även inom andra vetenskaper till exempel inom elektrofysik och geologi. Inom geologi används harmoniskt medelvärde för att kunna bestämma vattengenomsläppigheten i olika jordarter. Resistansen i parallelkoppling definieras med harmoniskt medelvärde, men det harmoniska medelvärdet måste delas med antalet resistorer som är parallella.
Exempel
Antag att en person färdas sträckorna s1,..., sN med hastigheterna v1,..., vN. Det är omedelbart uppenbart att genomsnittshastigheten v för hela resan ges av det viktade harmoniska medelvärdet
![v = \sum_{i=1}^n{s_i} \left[ \sum_{i=1}^n{s_i v_i^{-1}} \right]^{-1}.](/w/images/sv.rilpedia.org/math/6/1/3/6134d45b4f9e69f178f4108346d44e09.png)
Om vi vill t.ex räkna medelhastigheten till en bil som kör en 120 km lång sträcka fram och tillbaka mellan hemmet och sommarstugan, först med hastigheten 60 km/h till sommarstugan och sedan tillbaka hem med hastigheten 120 km/h. Då blir medelhastigheten lika med det harmoniska medelvärdet 80 km/h, inte det aritmetiska medelvärdet som är 90 km/h. Anledningen till detta är att det tar två timmar att köra 120 km med hastigheten 60 km/h, och att köra samma sträcka med farten 120 km/h tar bara en timme. Totalt har bilen kört 240 km under förloppet av 3 timmar, och om vi delar 240km jämnt på 3 timmar blir svaret 80 km/h, som är lika med det harmoniska medelvärdet.

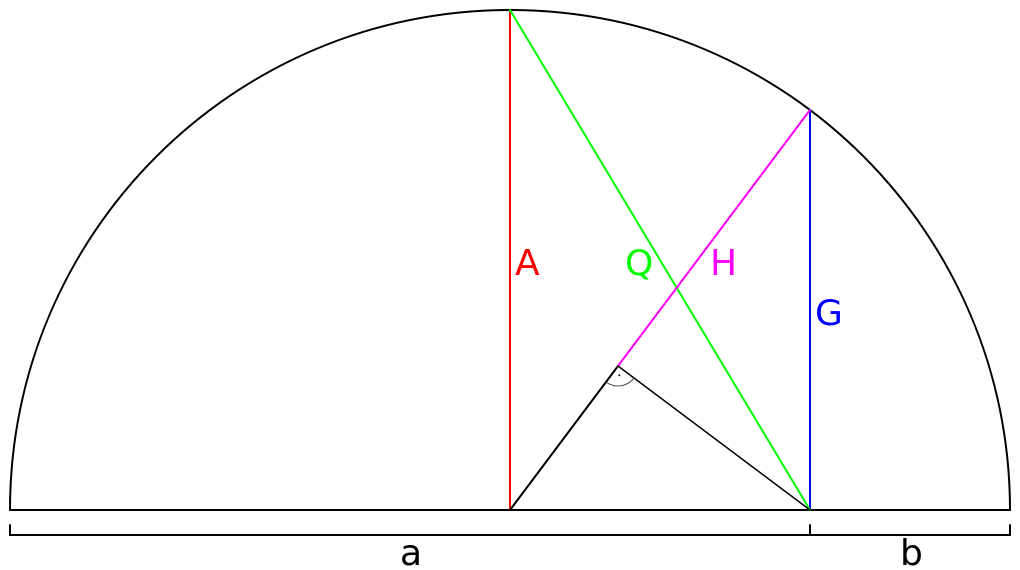
En bild av förhållandet mellan medelvärdena
Denna bild visar hur de olika medelvärdena konstrueras geometriskt.
A visar punkten vart vi hamnar på halvcirkeln, då vi beräknar det aritmetiska medelvärdet av två tal, a och b.
På samma sätt visar H punten det harmoniska medelvärdet av dessa två tal och G det geometriska medelvärdet.
Q är beteckningen för den kvardatiska medelvärdet.
Anmärkning
Bilden visar relationen mellan medelvärdena vara sann i alla situationer.