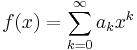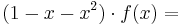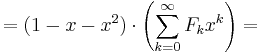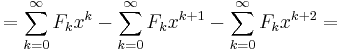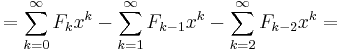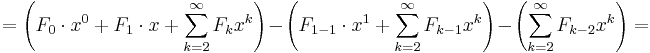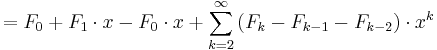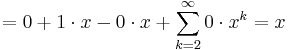Genererande funktion

Från Rilpedia

Version från den 2 mars 2009 kl. 15.53 av VolkovBot (Diskussion)
(skillnad) ← Äldre version | Nuvarande version (skillnad) | Nyare version → (skillnad)
Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Definition

Den genererande funktionen 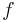f\ till talföljden 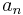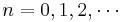a_n\ , n = 0, 1, 2, \cdots , definieras som

f(x)=\sum _{k=0}^\infty a_k x^k

Ofta är f bara definierad i ett intervall runt origo (ibland bara i en punkt), nämligen när summan bara konvergerar där. Det är då mer fruktbart att betrakta f som en formell potensserie snarare än en funktion.

Exempel

Den genererande funktionen till Fibonacciföljden 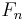F_n\ kan bestämmas som följer:

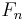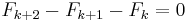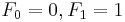
F_n\ definieras av rekursionen F_{k+2}-F_{k+1}-F_k=0\ , och F_0=0, F_1=1\

Genom att sätta 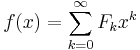f(x)=\sum _{k=0} ^\infty F_k x^k kan vi ställa upp

(1 - x - x^2) \cdot f(x) =

Substituera f(x)

= (1 - x - x^2) \cdot \left(\sum _{k=0} ^\infty F_k x^k\right) =

Multiplicera in i parentesen

= \sum _{k=0}^\infty F_k x^{k}- \sum _{k=0}^\infty F_k x^{k+1}- \sum _{k=0}^\infty F_k x^{k+2} =

Förskjut indexen med 0, 1 respektive 2 steg

= \sum _{k=0}^\infty F_k x^{k}- \sum _{k=1}^\infty F_{k-1} x^{k}- \sum _{k=2}^\infty F_{k-2} x^{k} =

Ta ut k=0 och k=1

= \left(F_0 \cdot x^0 + F_1 \cdot x + \sum _{k=2}^\infty F_k x^{k}\right) - \left(F_{1-1} \cdot x^1 + \sum _{k=2}^\infty F_{k-1} x^{k}\right)-\left(\sum _{k=2}^\infty F_{k-2} x^{k}\right) =

Slå ihop resterande summor

= F_0 + F_1 \cdot x - F_0 \cdot x + \sum _{k=2}^\infty \left(F_{k} - F_{k-1} - F_{k-2}\right) \cdot x^{k}

Sätt in F_0 = 0, F_1 = 1 och rekursionen

= 0 + 1 \cdot x - 0 \cdot x + \sum _{k=2}^\infty 0 \cdot x^{k} = x

Alltså gäller

f(x) = \frac{x}{1 - x - x^2}
Hämtad från "https://sv.rilpedia.org/wiki/Genererande_funktion"
Personliga verktyg