Liealgebra
Från Rilpedia
En Liealgebra är en algebraisk struktur, vars största användningsområde
är studiet av geometriska objekt såsom Liegrupper och differentierbara mångfalder.
Begreppet "Liealgebra" (döpt efter Sophus Lie, uttalat "li") infördes av Hermann Weyl under 1930-talet. I äldre texter används begreppet infinitesimal grupp.
Definition
En liealgebra är en viss sorts algebra över en kropp; den är ett vektorrum g över någon kropp K tillsammans med en binär operation [·, ·] : g × g → g, som kallas liebracket, vilken uppfyller följande villkor:
- Egenskap 1: Bilinjäritet:
- för alla a, b
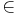 K och alla x, y, z
K och alla x, y, z 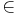 g.
g.
- Egenskap 2: För alla x
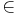 g gäller:
g gäller:
- Egenskap 3: Jacobi-identiteten:
- för alla x, y, z
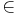 g.
g.
Observera att första och andra egenskapen medför att
för alla x, y 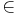 g ("anti-symmetri"). Å andra sidan medför antisymmetri egenskap nummer 2 om det gäller att kroppen K inte är av karaktäristik 2. En Liealgebra med andra egenskapen utbytt mot antisymmetri kallas för en kvasi-Liealgebra.
g ("anti-symmetri"). Å andra sidan medför antisymmetri egenskap nummer 2 om det gäller att kroppen K inte är av karaktäristik 2. En Liealgebra med andra egenskapen utbytt mot antisymmetri kallas för en kvasi-Liealgebra.
Observera också att multiplikationen som ges av liebracketen inte i allmänhet är associativ, dvs, [[x,y],z] behöver inte vara lika med [x,[y,z]]. Därför är Liealgebror inte ringar eller associativa ringar i den vanliga meningen.
Exempel
Ett konkret exempel på en Liealgebra är 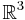 med vektorprodukt som bracketoperation. Även algebran av nxn-matriser är en Liealgebra med kommutatoroperationen [A,B] = AB − BA som bracketoperation. Mer allmänt gäller att varje associativ algebra blir en Liealgebra under kommutatoroperationen.
med vektorprodukt som bracketoperation. Även algebran av nxn-matriser är en Liealgebra med kommutatoroperationen [A,B] = AB − BA som bracketoperation. Mer allmänt gäller att varje associativ algebra blir en Liealgebra under kommutatoroperationen.
Referenser
- Erdmann, Karin & Wildon, Mark. Introduction to Lie Algebras, 1st edition, Springer, 2006. ISBN 1-84628-040-0
- Brian C. Hall Lie Groups, Lie Algebras, and Representations: An Elementary Introduction, 1st edition, Springer, 2006. ISBN 0-387-40122-9
- Humphreys, James E. Introduction to Lie Algebras and Representation Theory, Second printing, revised. Graduate Texts in Mathematics, 9. Springer-Verlag, New York, 1978. ISBN 0-387-90053-5
- Jacobson, Nathan, Lie algebras, Republication of the 1962 original. Dover Publications, Inc., New York, 1979. ISBN 0-486-63832-4
- Kac, Victor G. et. al. Course notes for MIT 18.745: Introduction to Lie Algebras, http://www-math.mit.edu/~lesha/745lec/
- Varadarajan, V. S. Lie Groups, Lie Algebras, and Their Representations, 1st edition, Springer, 2004. ISBN 0-387-90969-9




![[a x + b y, z] = a [x, z] + b [y, z], \quad [z, a x + b y] = a[z, x] + b [z, y]](/w/images/sv.rilpedia.org/math/5/0/d/50d637f47c6fa9abec81c24abb5b7872.png)
![[x,x]=0 \,](/w/images/sv.rilpedia.org/math/8/a/4/8a400b53b3d4c1e93dcd2a77e580d633.png)
![[x,[y,z]] + [y,[z,x]] + [z,[x,y]] = 0 \quad](/w/images/sv.rilpedia.org/math/6/9/e/69ee53d21fe7eb5e7b8ed7938cb8cab0.png)
![[x,y] = -[y,x] \,](/w/images/sv.rilpedia.org/math/c/e/d/cedc8d491f577aef737493a4a33f11e5.png)