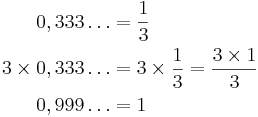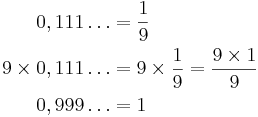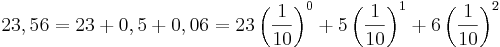0,999...

Från Rilpedia

Version från den 11 maj 2009 kl. 18.49 av MelancholieBot (Diskussion)
(skillnad) ← Äldre version | Nuvarande version (skillnad) | Nyare version → (skillnad)
Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif
999 Perspective.png

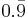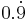Inom matematiken representerar 0,999… (även benämnt som 0.\bar{9} eller 0.\dot{9}) en periodisk decimalutveckling som är exakt lika med talet 1. Med andra ord, symbolerna 0,999… och 1 representerar samma reella tal. Matematikerna har formulerat ett antal matematiska bevis för denna identitet, som varierar genom deras nivå av stringens, föredragen konstruktion av de reella talen, bakgrundsantaganden, historiskt sammanhang och målgrupp.

Likheten 0,999… = 1 har länge lärts ut i läroböckerna, och under de senaste årtiondena har forskare inom matematikpedagogik studerat mottagandet bland studenter, som ofta ljudligt motsätter sig denna likhet. Studenternas resonemang kan baseras på förväntningen att infinitesimala kvantiteter skulle finnas, att aritmetiken kanske är felaktig, eller helt enkelt att 0,999… skulle ha en sista 9:a. Dessa idéer är falska när det kommer till reella tal, vilket kan bevisas genom att explicit skapa de reella talen från de rationella talen, och ur sådana konstruktioner följer också direkt att 0,999… = 1. Samtidigt kan vissa av de intuitiva fenomenen studenter ibland väntar sig framträda i andra talsystem. Det finns även system där ett objekt, som skulle kunna kallas för "0,999…" är strikt mindre än 1.

Att talet 1 har två decimalexpansioner är inte någon säregenhet för decimalsystemet. Samma fenomen påträffas i alla heltalsbaser, och matematiker har även studerat sätt att skriva 1 i icke-heltalsbaser. Fenomenet är inte heller unikt för 1: varje ändlig decimalexpansion har en tvilling med efterföljande 9:or. De facto innehåller alla positionssystem ett oändligt antal tal som saknar unik decimalrepresentation. Dessa identiteter har använts för att bättre förstå mönster inom decimalutvecklingen för bråktal och strukturen hos en enkel fraktal, Cantormängden. De bör också beaktas i det klassiska beviset för att mängden av reella tal är överuppräknelig.

Innehåll

Bevis

Bråktalsbevis

\begin{align} 0,333\dots &= \frac{1}{3} \\ 3 \times 0,333\dots &= 3 \times \frac{1}{3} = \frac{3 \times 1}{3} \\ 0,999\dots &= 1 \end{align}

\begin{align} 0,111\dots &= \frac{1}{9} \\ 9 \times 0,111\dots &= 9 \times \frac{1}{9} = \frac{9 \times 1}{9} \\ 0,999\dots &= 1 \end{align}

Algebraiskt bevis

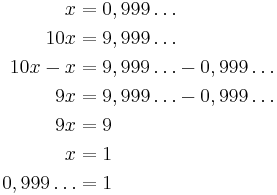
\begin{align} x &= 0,999\ldots \\ 10 x &= 9,999\ldots \\ 10 x - x &= 9,999\ldots - 0,999\ldots \\ 9x &= 9,999\ldots - 0,999\ldots \\ 9x &= 9 \\ x &= 1 \\ 0,999\ldots &= 1 \end{align}

Bevis med oändliga serier

Ett reellt tal a kan uttryckas som en summa av en, möjligtvis oändlig, serie:

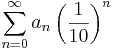\sum_{n=0}^{\infty} a_n \left(\frac{1}{10}\right)^n .

Där a0 är delen av a som är större än 1 och ak är decimalen på plats k. Exempelvis kan talet 23,56 uttryckas som:

23,56 = 23 + 0,5 + 0,06 = 23 \left(\frac{1}{10}\right)^0 + 5 \left(\frac{1}{10}\right)^1 + 6 \left(\frac{1}{10}\right)^2

Vi kan då uttrycka 0,999... som:

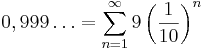0,999\dots = \sum_{n = 1}^{\infty} 9 \left(\frac{1}{10}\right)^n .

Vilket är en geometrisk serie, där vi har följande sats:

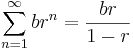\sum_{n=1}^{\infty} br^n = \frac{br}{1-r} om |r| < 1 \,.

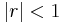I fallet 0,999... är 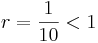r = \frac{1}{10} < 1 så att:

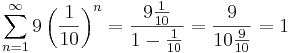\sum_{n = 1}^{\infty} 9 \left(\frac{1}{10}\right)^n = \frac{9\frac{1}{10}}{1-\frac{1}{10}} = \frac{9}{10\frac{9}{10}} = 1.

Detta bevis presenterades redan 1770 av Leonard Euler.

Se även

Hämtad från "https://sv.rilpedia.org/wiki/0,999..."
Personliga verktyg