Karush-Kuhn-Tucker villkor

Från Rilpedia

Version från den 11 april 2009 kl. 21.02 av Louperibot (Diskussion)
(skillnad) ← Äldre version | Nuvarande version (skillnad) | Nyare version → (skillnad)
Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Karush-Kuhn-Tucker villkor (eller KKT-villkor) är ett villkor som måste vara uppfyllt för att en punkt ska vara en optimallösning till ett optimeringsproblem. Villkoret är nödvändigt men inte tillräckligt, dvs. om villkoret är uppfyllt behöver inte punkten vara optimum, men optimum uppfyller villkoret. Förutom optimum uppfyller även lokala optimum och sadelpunkter villkoret.

Villkoren

Antag att man har en funktion som ska minimeras med vissa bivillkor.

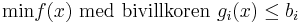
\mbox{min} f(x) \mbox{ med bivillkoren } g_i(x) \le b_i

I sådana fall uppfyller en punkt som är funktionens optimum (punkten x * ) följande villkor:

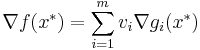
\nabla f(x^*) = \sum_{i=1}^m v_i \nabla g_i(x^*)

Koefficienten är här 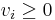v_i \ge 0

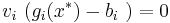v_i \ (g_i (x^*) - b_i \ ) = 0 (villkor för att endast aktiva bivillkor ska påverka)

Emedan optimum måste vara en tillåten punkt krävs det att punkten uppfyller bivillkoren

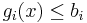
g_i(x) \le b_i

Källor

  • Jan Lundgren, Mikael Rönnquist, Peter Värbrand: Optimeringslära, Studentlitteratur, Lund 2003, 2. upplagan. ISBN 91-44-03104-1. 
Hämtad från "https://sv.rilpedia.org/wiki/Karush-Kuhn-Tucker_villkor"
Personliga verktyg