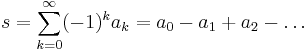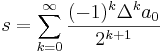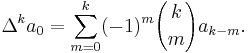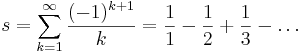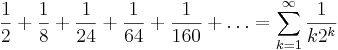Eulers transform
Från Rilpedia
Version från den 25 oktober 2006 kl. 20.49 av Andejons (Diskussion)
Eulers transform, uppkallad efter Leonhard Euler, är inom matematik en metod för att förbättra konvergensen hos alternerande serier. En konvergent alternerande serie
transformeras med denna metod till
där Δ är en differensoperator sådan att
Eulers transform är en speciell tillämpning av binomialtransformen.
Exempel
Den långsamt konvergerande alternerande harmoniska serien
med summan s = ln 2 omvandlas med Eulers transform till
som konvergerar betydligt snabbare.
Källor
- Milton Abramowitz & Irene A. Stegun, Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, s. 16
- Lennart Råde & Bertil Westergren, Mathematics Handbook for Science and Engineering, Studentlitteratur 2004, s. 421