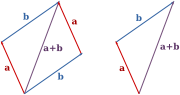
Vektoraddition

Från Rilpedia

Version från den 17 juni 2007 kl. 22.55 av Pieter Kuiper (Diskussion)
(skillnad) ← Äldre version | Nuvarande version (skillnad) | Nyare version → (skillnad)
Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif
Två geometriska sätt att addera två vektorer.

Vektoraddition beskriver hur man generaliserar addition till att även gälla vektorer.

Man kan, i många fall, med fördel tänka sig en vektor som en pinne mellan origo och en angiven koordinat. Den intuitiva förklaringen av vektoraddition skulle då vara att sätta ihop flera sådana pinnar till en lång krokig pinne för att få en ny vektor mellan origo och den krokiga pinnens ändpunkt. Rent matematiskt innebär detta att till exempel en tredimensionell vektor 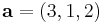\mathbf{a} = (3,1,2) adderad med en vektor 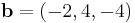\mathbf{b} = (-2,4,-4) bildar resultanten:

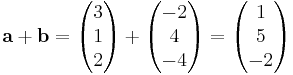\mathbf{a}+\mathbf{b}=\begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + \begin{pmatrix} -2 \\ 4 \\ -4 \end{pmatrix} = \begin{pmatrix} 1 \\ 5 \\ -2 \end{pmatrix},

eller det generella fallet

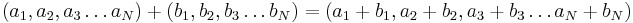(a_1,a_2,a_3 \dots a_N) + (b_1,b_2,b_3 \dots b_N) = (a_1+b_1,a_2+b_2,a_3+b_3 \dots a_N+b_N)\,.

Ordningen i vilken man adderar vektorer spelar ingen roll: vektoraddition är kommutativ.

Hämtad från "https://sv.rilpedia.org/wiki/Vektoraddition"
Personliga verktyg