Omgivning

Från Rilpedia

Version från den 28 mars 2009 kl. 00.19 av Calle (Diskussion)
(skillnad) ← Äldre version | Nuvarande version (skillnad) | Nyare version → (skillnad)
Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif
En omgivning V till punkten p. V innehåller en öppen mängd som innehåller p.
En rektangel V som inte är en omgivning till p.

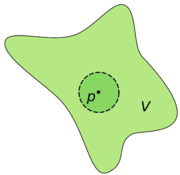
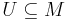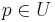Inom topologin sägs en mängd M vara en omgivning till en punkt p om det finns en öppen mängd U så att U\subseteq M och p\in U. Detta är ekvivalent med att p tillhör det inre av M.

Ofta talar man om en öppen omgivning till en punkt p, vilket är en omgivning som är en öppen mängd, eller ekvivalent, en öppen mängd M så att 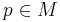p\in M

I ett metriskt rum är B(p,t), mängden av punkter med avstånd mindre än t till punkten p, en öppen omgivning till p.

Exempel på användningar av begreppet omgivning

  • En delmängd U till ett topologiskt rum T är öppen om och endast om varje punkt har en öppen omgivning.
  • En funktion f sägs vara lokalt begränsad om varje punkt har en omgivning i vilken f är begränsad
  • Ett topologiskt rum sägs vara lokalt sammanhängande i en punkt p om varje omgivning till p har en sammanhängande delomgivning.
  • I ett topologiskt vektorrum genereras topologin av den öppna omgivningarna till punkten 0.
Hämtad från "https://sv.rilpedia.org/wiki/Omgivning"
Personliga verktyg