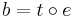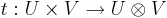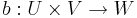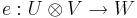Bilinjär
Från Rilpedia
Version från den 22 november 2008 kl. 19.25 av 81.231.250.247 (Diskussion)
Inom linjär algebra sägs en avbildning i två variabler vara bilinjär om den är linjär i varje variabel var för sig.
Definition
En avbildning 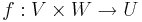 där U,V,W är vektorrum över en kropp K, sägs vara bilinjär om
där U,V,W är vektorrum över en kropp K, sägs vara bilinjär om
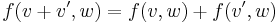

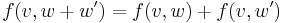

för alla 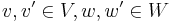 och
och 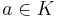 .
.
Exempel
- Matrismultiplikation är en bilinjär avbildning
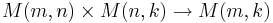
- Kryssprodukten är en bilinjär avbildning
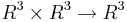 .
. - Applikationsoperatorn som till ett element
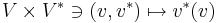 är bilinjär.
är bilinjär. - Kovarians är bilinjär
Egenskaper
De bilinjära avbildningarna utgör ett linjärt delrum till rummet av linjära avbildningar 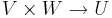
Tensorprodukter används för att klassificera bilinjära avbildningar; närmare bestämt, det finns en kanonisk avbildning
så att för varje bilinjär avbildning
så finns en unik avbildning
så att