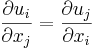Sluten differentialform

Från Rilpedia

Version från den 23 november 2008 kl. 13.57 av LA2-bot (Diskussion)
(skillnad) ← Äldre version | Nuvarande version (skillnad) | Nyare version → (skillnad)
Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

En differentialform 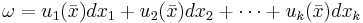\omega = u_1(\bar{x})dx_1 + u_2(\bar{x})dx_2 + \cdots + u_k(\bar{x})dx_k av klass 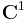\textbf{C}^1 (minst en gång kontinuerligt deriverbar) säges vara sluten om

\frac{\partial u_i}{\partial x_j} = \frac{\partial u_j}{\partial x_i}

eller, i annan formalism, om dω = 0. d betecknar här den yttre derivatan. Notera att om ω är en k-form, så är dω en k+1-form.

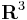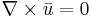Vi ser att en differentialform i \textbf{R}^3 är sluten om och endast om det motsvarande vektorfältet är rotationsfritt (\nabla \times \bar{u} = 0).

Relation mellan slutna och exakta differentialformer

En exakt differentialform är alltid sluten, eftersom d2ω = 0 för varje differentialform ω. I ett enkelt sammanhängande område, och i synnerhet i ett stjärnformat område, är varje sluten differentialform exakt enligt Poincarés lemma.

I allmänhet gäller dock inte att varje sluten differentialform är exakt, och inom topologi studeras detta med hjälp av de Rham-kohomologi.

de Rham-kohomologi

Låt M vara en mångfald, och låt mängden av k-former på M betecknas med Ω(M). Vi låter nu dk beteckna den yttre derivatan, verkande på k-former på M: 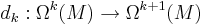d_k: \Omega^{k}(M) \rightarrow \Omega^{k+1}(M)

Den k-te de Rham-kohomologigruppen 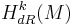H^k_{dR}(M) definieras nu som 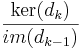\frac{\ker(d_k)}{im(d_{k-1})} , eller med andra ord mängden av slutna differentialformer modulo exakta former.

Exempel: För en n-sfär 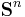\mathbf{S}^n gäller att 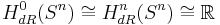H^0_{dR}(S^n) \cong H^n_{dR}(S^n) \cong \mathbb{R}, medan 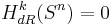H^k_{dR}(S^n) = 0 för alla andra k. För sådana k är alltså alla slutna differentialformer exakta.

Hämtad från "https://sv.rilpedia.org/wiki/Sluten_differentialform"
Personliga verktyg
På andra språk