Likformig konvergens
Från Rilpedia
Version från den 17 september 2008 kl. 12.21 av JAnDbot (Diskussion)
Inom matematiken sägs en sekvens av funktioner 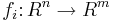 konvergera likformigt mot en funktion f på en mängd I om följande villkor uppfylls:
konvergera likformigt mot en funktion f på en mängd I om följande villkor uppfylls:
- För varje ε > 0 så finns ett
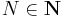 så att för alla
så att för alla 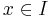 så gäller att n > N medför
så gäller att n > N medför 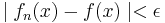
Detta skall jämföras med villkoret att sekvensen endast konvergerar, som lyder enlig följande:
- För varje
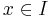 och ε > 0 så finns ett
och ε > 0 så finns ett 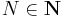 så att n > N medför
så att n > N medför 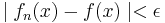
Exempel
- Följden
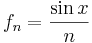 konvergerar likformigt mot 0 på R.
konvergerar likformigt mot 0 på R. - Följden
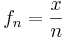 konvergerar mot 0 på R, men inte likformigt
konvergerar mot 0 på R, men inte likformigt - Följden fn = xn konvergerar, men inte likformigt, mot funktionen g på intervallet [0,1] där g är funktionen som har värdet 1 i punkten 1 och värdet 0 annars.
Egenskaper
Likformig konvergens är ett viktigt begrepp i analysens grunder, eftersom det används för att sluta sig till egenskaper hos en funktion f som är gränsvärdet av en följd fi utifrån egenskaper hos funktionerna fi. Till exempel gäller att en om en följd av kontinuerliga funktioner konvergerar likformigt mot en funktion, är även denna funktion kontinuerlig. Som exempel 3 ovan visar behöver detta inte vara sant så sekvensen inte konvergerar likformigt.



