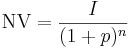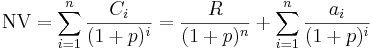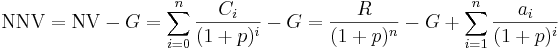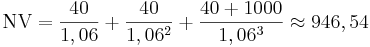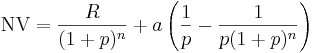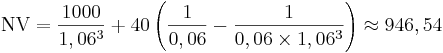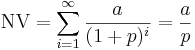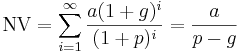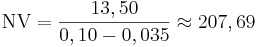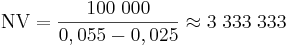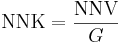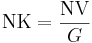Nuvärdemetoden

Från Rilpedia

Version från den 5 maj 2009 kl. 09.54 av 138.227.189.10 (Diskussion)

(skillnad) ← Äldre version | Nuvarande version (skillnad) | Nyare version → (skillnad)

Hoppa till: navigering, sök

Texten från svenska Wikipedia

Jämförelse mellan nuvärde och slutvärde.

Nuvärdemetoden, även känd som diskonteringsmetoden, kassaflödesmetoden och kapitalvärdemetoden, används för att fastställa en investerings lönsamhet. Hos större svenska företag och myndigheter är det kanske den vanligaste metoden^[1] för investeringskalkylering, tillsammans med pay off-metoden. Den är nära relaterad till en rad andra metoder, till exempel slutvärdemetoden, annuitetsmetoden och internräntemetoden.

Nuvärde, även kapitalvärde, är det beräknade värdet av en investerings framtida kassaflöde, diskonterade med hänsyn till en given kalkylräntesats.

Nettonuvärde är differensen mellan nuvärde och investeringskostnad.

Kapitalvärdekvot är en term som oftast används i betydelsen nettonuvärdekvot, det vill säga nettonuvärdet delat med investeringskostnad. Emellanåt kan uttrycket även betyda nuvärdekvot, vilket är nuvärdet delat med grundkostnad.

Översikt

En investerings kassaflöden och nuvärde.

Nuvärdemetoden går ut på att antingen beräkna en investerings nuvärde och jämföra detta med investeringskostnaden, eller beräkna nettonuvärdet direkt. Den första varianten är ofta den som beskrivs i, åtminstone äldre, svensk kurslitteratur. Den andra är vanlig i amerikansk kurslitteratur. I praktiken är de båda varianterna helt jämställda; man gör samma sak.

Nuvärdesberäkningen kan jämföras med att sätta in pengar på ett konto. Den besvarar frågan ”Hur mycket pengar måsta jag sätta in idag för att ha x mycket pengar om y år”. Om man vänder på frågan får man istället ett slutvärde. Beräkningen är som en ränta-på-ränta-beräkning, fast tvärtom. Nuvärdet av en enstaka framtida inbetalning (I) får man således genom följande formel (beteckningarna förklaras nedan):

$\mbox{NV} = { I \over (1+p)^n }$

Metoden kan användas både för att besluta om en viss investering ska genomföras, eller för att jämföra olika investeringsalternativ. Det går dock bara att jämföra alternativ med lika lång ekonomisk livslängd. Om livslängden är olika, är annuitetsmetoden bättre; den slår i princip ut nuvärdet över livslängden.

En investering är lönsam om nuvärdet är större än investeringskostnaden, det vill säga nettonuvärdet är större än noll. Vid en jämförelse kan det antingen vara det alternativ som har störst nuvärde, störst nettonuvärde eller störst kapitalvärdekvot som är mest lönsam.

Beräkningar

För beräkningar av nuvärde och nettonuvärde behöver vi vissa indata. I den här artikeln används följande beteckningar:

NV	Nuvärde
NNV	Nettonuvärde
q	Kapitalvärdekvot. Kan antingen beräknas som nettonuvärdekvot, NNK, eller nuvärdekvot NK.
I	Inbetalningar.
U	Utbetalningar.
G	Investeringskostnad (grundinvestering).
a	Årligt inbetalningsöverskott (I - U). Om dessa är olika anges de som a_i, där i anger vilket år det fråga om.
R	Restvärde. Värdet av maskinen/värdepappret/tillgången vid beräkningens slut.
p	Kalkylränta. Vilken räntesats vi ska använda för diskonteringen.
n	Investeringens ekonomiska livslängd.
C	Totalt årligt kassaflöde, vilket inkluderar investeringskostnader, inbetalningsöverskott och restvärde. För ett visst år anges det C_i. C₀ är kassaflödet vid investeringstillfället (oftast = -G).
g	Tillväxtfaktor.

Beräkningen av nuvärde och nettonuvärde görs enligt nedanstående formler.

$\mbox{NV} = \sum_{i=1}^n { C_i \over (1+p)^i } = { R \over (1+p)^n } + \sum_{i=1}^n { a_i \over (1+p)^i }$

$\mbox{NNV} = \mbox{NV} - G = \sum_{i=0}^n { C_i \over (1+p)^i } - G = { R \over (1+p)^n } - G + \sum_{i=1}^n { a_i \over (1+p)^i }$

Exempel: Obligation

Du vill spara en summa pengar i statsobligationer under 3 år. Nya treåriga obligationer ger 6% ränta, men du kan även köpa 7 år gamla obligationer som löpte över 10 år. De hade ett nominellt belopp på 1000 kronor till 4% ränta, det vill säga ger 40 kronor om året. Hur mycket ska du betala för dem? Anta att det är i början av året, och räntan betalas vid årsskiftet.

$\mbox{NV} = { 40 \over 1,06 } + { 40 \over 1,06^2 } + { { 40 + 1000 } \over 1,06^3 } \approx 946,54$

Du ska alltså inte betala mer än 946 kronor styck. Om priset är lägre än så är då mer lönsamma än nya obligationer. Vid priset 938 kronor blir nettonuvärdet 8,54 kronor, och kapitalvärdekvoten ungefär 0,9%.

Återkommande belopp

Om alla inbetalningsöverskott är lika stora, som i exemplet ovan, går det att använda en snabbare formel. Den använder sig av annuitetsfaktorn.

$\mbox{NV} = { R \over (1+p)^n } + a \left ( { 1 \over p } - { 1 \over { p (1+p)^n } } \right )$

Exemplet skulle då ge följande uträkning:

$\mbox{NV} = { 1000 \over 1,06^3 } + 40 \left ( { 1 \over 0,06 } - { 1 \over { 0,06 \times 1,06^3 } } \right ) \approx 946,54$

Den här varianten är lättare om investeringens ekonomiska livslängd är lång.

Eviga investeringar

Vissa långsiktiga investeringar kan ha så lång livslängd att de kan approximeras som eviga. Det kan exempelvis gälla aktier. En aktiekurs skulle kunna vara en värdering av framtida utdelningar. Det kan även gälla fastigheter, där hyran kan ses som en ”evig” inkomst. I sådana fall faller restvärdet bort, och beräkningen blir en geometrisk serie.

$\mbox{NV} = \sum_{i=1}^\infty { a \over { (1+p)^i } } = { a \over p }$

Ofta är det relevant att ta hänsyn till att olika inkomster och utgifter ökar över tiden. Då kan Gordons formel, som tar hänsyn även till tillväxtfaktorn, användas.

$\mbox{NV} = \sum_{i=1}^\infty { { a (1+g)^i } \over { (1+p)^i } } = { a \over { p - g } }$

Exempel: Aktie

En riktkurs för en aktie kan beräknas med ovanstående formel. Säg att den genomsnittliga utdelningen för det senaste året, innevarande år och kommande år är 13,50 kronor. Företaget är moget, och utdelningen växer kanske med 3,5% om året i genomsnitt. Du vill dock ha 10% avkastning för att täcka för kursfluktuationer.

$\mbox{NV} = { 13,50 \over { 0,10 - 0,035 } } \approx 207,69$

En lämplig riktkurs kan då vara 208 kronor.

Exempel: Fastighet

Även priset på en fastighet kan beräknas med ovanstående formel. Antag att en viss given fastighet ger ett årligt driftnetto, det vill säga hyra minus driftskostnader, på 100.000 kronor. Du har ett avkastningskrav på 5,5% och räknar med en inflation på 2,5%.

$\mbox{NV} = { {100\;000} \over { 0,055 - 0,025 } } \approx 3\;333\;333$

Ett lämpligt pris bör vara 3,3 miljoner kronor.

Kapitalvärdekvot

Vid jämförelser mellan olika investeringar kan det vara mer intressant vilken investering som ger mest pengar tillbaka per satsad krona, än det absoluta beloppet utan hänsyn till grundinvesteringen. Ett sätt att göra det här på är att dela nuvärdet eller nettonuvärdet med grundinvestering. Detta ger nettonuvärdekvot respektive nuvärdekvot. Båda begreppen kallas ibland för kapitalvärdekvot, som alltså kan vara tvetydigt.

Nettonuvärdekvoten (NNK) och nuvärdekvoten (NK) beräknas alltså på följande sätt:

$\mbox{NNK} = { \mbox{NNV} \over G }$

$\mbox{NK} = { \mbox{NV} \over G }$

För att en investering ska vara lönsam, ska nettonuvärdekvoten vara över noll och nuvärdekvoten ska vara över ett. Det alternativ som har högst kvot är mest lönsam.

Framförallt nettonuvärdekvoten används exempelvis vid investeringsbedömningar av infrastruktur. Kvoterna används bland annat även för att ranka olika produktionsalternativ för nya produkter.

Se även

Externa länkar

Referenser

Fotnoter

↑ Hur vanliga olika kalkyleringsmetoder är bekräftas bland annat av en C-uppsats på Karlstads Universitet, som även går igenom tidigare undersökningar i frågan. Uppsatsen behandlar dock endast industriella investeringar i företag. Finansiella investeringar för företag, privatpersoner och organisationer behandlas inte. Se vidare Persson, Karin; Gustaf Posse, Maria Rosner: Investeringsbedömning - En studie om investeringsbedömningen i ett antal svenska tillverkande företag, Karlstads Universitet, Karlstad 2007 (PDF) (svenska). Hämtat 14 juni 2008.

Tryckta Källor

Nurmis, Peter; Ogi Chun: Övningskompendium, Kalkylering & rationalitet, Stockholms Universitet/Reproenheten, Stockholm [1994] 1997 "Formler",, 3:e uppl. (svenska).
Andersson, Göran: Kalkyler som beslutsunderlag, Studentlitteratur, Lund [1983] 2001, 5:e uppl. (svenska). ISBN 91-44-01910-6.
Brealey, Richard A.; Stewart C. Myers: Principles of corporate finance, McGraw-Hill Companies, Inc., [1981] 1996, fifth ed. (engelska). ISBN 0-07-114053-0.

Webbkällor

Kassaflödesvärderingar eller ”kassa” flödesvärderingar (PDF) (13 juni 2008).

[vanlig-0] Hur vanliga olika kalkyleringsmetoder är bekräftas bland annat av en C-uppsats på Karlstads Universitet, som även går igenom tidigare undersökningar i frågan. Uppsatsen behandlar dock endast industriella investeringar i företag. Finansiella investeringar för företag, privatpersoner och organisationer behandlas inte. Se vidare Persson, Karin; Gustaf Posse, Maria Rosner: Investeringsbedömning - En studie om investeringsbedömningen i ett antal svenska tillverkande företag, Karlstads Universitet, Karlstad 2007 (PDF) (svenska). Hämtat 14 juni 2008.

[1]