Funktionsutveckling

Från Rilpedia

Version från den 9 september 2008 kl. 10.44 av LA2-bot (Diskussion)
(skillnad) ← Äldre version | Nuvarande version (skillnad) | Nyare version → (skillnad)
Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Det finns olika sätt att representera funktioner. Dels kan uttrycket transformeras till olika "baser" (exempelvis Fourieranalys) eller så approximeras i enstaka punkter (Taylorutveckling eller implicita funktionssatsen).


Några vanliga utvecklingar
Namn Formel Disciplin
Taylorserie 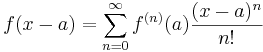f(x - a) = \sum_{n = 0}^{\infty}f^{(n)}(a)\frac{(x - a)^n}{n!}
Laurentserie 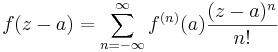f(z - a) = \sum_{n = -\infty}^{\infty}f^{(n)}(a)\frac{(z - a)^n}{n!} Komplex analys et al
Virialutveckling 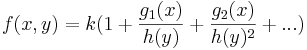f(x, y) = k(1+\frac{g_1(x)}{h(y)} + \frac{g_2(x)}{h(y)^2} + ...) Termodynamik
Klusterutveckling 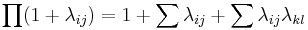\prod(1+\lambda_{ij}) = 1 + \sum \lambda_{ij} + \sum \lambda_{ij}\lambda_{kl} Kvantmekanik

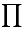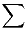I klusterutvecklingen motsvarar \prod och \sum sekvenserna: \prod(1+\lambda_{ij}) = [(1 + \lambda_{12})(1 + \lambda_{13})\cdot\cdot\cdot(1 + \lambda_{1,N})][(1 + \lambda_{21})(1+\lambda_{23})\cdot\cdot\cdot][...][(1 + \lambda_{N-1,N})] \sum_{i,j,k,l,...}\lambda_{ij}\lambda_{kl}\cdot\cdot\cdot = \sum_{i = 1}^N \sum_{\begin{matrix}j = 1\\ j\ne i \end{matrix}}^{N} \sum_{\begin{matrix}k = 1\\ k\ne j \\ k\ne i \end{matrix}}^{N} \sum_{\begin{matrix}l = 1\\ l \ne k \\l\ne j \\ l\ne i \end{matrix}}^{N} \cdot\cdot\cdot[\lambda_{ij}][\lambda_{kl}]\cdot\cdot\cdot


E-to-the-i-pi.svg Denna matematik-relaterade artikel är bara påbörjad. Du kan hjälpa till genom att utöka den.
Hämtad från "https://sv.rilpedia.org/wiki/Funktionsutveckling"
Personliga verktyg