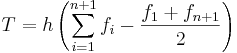Trapetsmetoden

Från Rilpedia

Version från den 10 april 2009 kl. 14.57 av Alecs.bot (Diskussion)

(skillnad) ← Äldre version | Nuvarande version (skillnad) | Nyare version → (skillnad)

Hoppa till: navigering, sök

Texten från svenska Wikipedia

Integrering av en graf

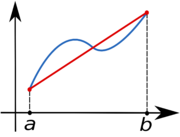
Trapetsmetoden (även trapetsregeln) används för att räkna ut integral av en graf numeriskt, man tar värden för grafen vid kända punkter och bildar trapetser. Sedan räknar man ut arean på dessa trapetser och har alltså integralens uppskattade värde.

Trapetsregeln i ett allmänt fall med varierande steglängd h.
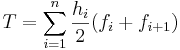
$T=\sum_{i=1}^{n} \frac{h_{i}}{2}(f_{i}+f_{i+1})$

Om n=4 och h fixt blir summan
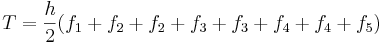
$T=\frac{h}{2}(f_{1}+f_{2} + f_{2}+f_{3}+ f_{3}+f_{4} + f_{4}+f_{5} )$

Vilket ger att summan som används i numeriska metoder ofta skrivs som.