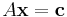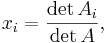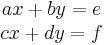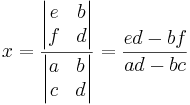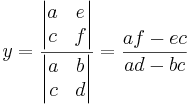Cramers regel
Från Rilpedia
Cramers regel är en sats inom linjär algebra, vilken ger lösningen till ett linjärt ekvationssystem med hjälp av determinanter. Namngiven efter Gabriel Cramer (1704-1752).
Beräkningsmässigt är metoden ineffektiv eftersom flera ekvationsevalueringar är nödvändiga. Den är därför inte använd i större grad inom praktiska tillämpningar. Men satsen har en större teoretisk innebörd då metoden ger ett explicit uttryck för lösningar av ekvationssystemet.
Ett ekvationssystem representeras i matrisnotation som
där A är en inverterbar kvadratisk matris och vektorn 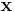 är en kolumnvektor.
är en kolumnvektor.
Satsen visar att
där Ai är matrisen med i:e kolumnen i A utbytt mot kolumnvektorn 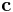 och xi den i:e komponenten i lösningsvektorn.
och xi den i:e komponenten i lösningsvektorn.
Exempel
Cramers metod är en bra hjälp för att lösa ekvationssystem som motsvarar en 2×2-matris:
(vilket motsvarar matrisnotationen
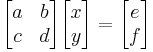 )
)
Lösningarna fås av satsen