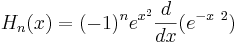Hermitepolynom

Från Rilpedia

Version från den 4 april 2009 kl. 12.33 av XZeroBot (Diskussion)

(skillnad) ← Äldre version | Nuvarande version (skillnad) | Nyare version → (skillnad)

Hoppa till: navigering, sök

Texten från svenska Wikipedia

Hermitepolynomen, uppkallade efter franske 1800-talsmatematikern Charles Hermite, är en uppsättning ortogonala polynom hemmahörande i Hilbertrummet 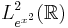$L^2_{e^{x^2}}(\mathbb{R})$ . De betecknas H_n(x), där n är gradtalet. Med Rodrigues formel kan man generera det n-te polynomet.

$H_n(x)=(-1)^n e^{x^2}\frac{d}{dx}(e^{-x~2})$

Hermitepolynomen är även lösningen till ett Sturm-Liouville-problem, nämligen

y'' - 2 x y' + 2 n y = 0

De elva första Hermitepolynomen är:

H 0 (x) = 1

H 1 (x) = 2 x

H 2 (x) = 4 x 2 - 2

H 3 (x) = 8 x 3 - 12 x

H 4 (x) = 16 x 4 - 48 x 2 + 12

H 5 (x) = 32 x 5 - 160 x 3 + 120 x

H 6 (x) = 64 x 6 - 480 x 4 + 720 x 2 - 120

H 7 (x) = 128 x 7 - 1344 x 5 + 3360 x 3 - 1680 x

H 8 (x) = 256 x 8 - 3584 x 6 + 13440 x 4 - 13440 x 2 + 1680

H 9 (x) = 512 x 9 - 9216 x 7 + 48384 x 5 - 80640 x 3 + 30240 x

H 10 (x) = 1024 x 1 0 - 23040 x 8 + 161280 x 6 - 403200 x 4 + 302400 x 2 - 30240

Hermitepolynom

Från Rilpedia

Visningar

Personliga verktyg

Sök

Navigering

Bibeln

Övrigt

Verktygslåda

På andra språk