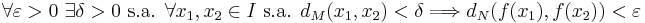Likformig kontinuitet
Från Rilpedia
Likformig kontinuitet är en strängare form av kontinuitet. Likformig kontinuitet är till skillnad mot kontinuitet en global egenskap, och är därför inte definierad för enskilda punkter. En funktion kan vara kontinuerlig i varje punkt i ett intervall utan att för den skull vara likformigt kontinuerlig på intervallet.
Informellt kan man säga att om en funktion är likformigt kontinuerlig så medför små förändringar i argumentet x små förändringar i f(x), oberoende av vilket x vi betraktar. För att kunna säga att en funktion f är likformig kontinuerlig krävs att f är definierad mellan rum som har mer struktur än bara en topologi. En sådan struktur kallas en likformig struktur. Typiska exempel på sådana rum är metriska rum samt topologiska grupper.
Definition
En funktion f : M → N definierad mellan metriska rum M och N, säges vara likformigt kontinuerlig om
Skillnaden mot vanlig kontinutet är att för likformigt kontinuerliga funktioner går det att finna ett δ som är användbart över hela intervallet.
Ett exempel på en funktion som är kontinuerlig, men inte likformigt kontinuerlig, är f(x)=1/x på intervallet (0,1]
Om en funktion är kontinuerlig på ett slutet intervall så är den också likformigt kontinuerlig på samma intervall.
Egenskaper
- Om M är ett kompakt metriskt rum är varje kontinuerlig funktion
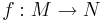 likformigt kontinuerlig, Heine-Cantors sats.
likformigt kontinuerlig, Heine-Cantors sats. - Om
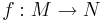 är likformigt kontinuerlig, så avbildas Cauchyföljder i M på Cauchyföljder i N.
är likformigt kontinuerlig, så avbildas Cauchyföljder i M på Cauchyföljder i N. - Likformig kontinuitet är, till skillnad från kontinuitet, en global egenskap hos en funktion.