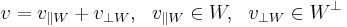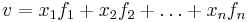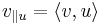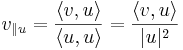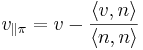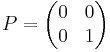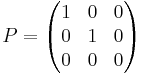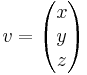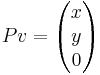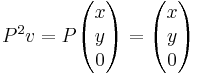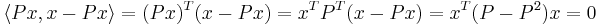Projektion (matematik)

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Inom matematikområdena linjär algebra och funktionalanalys är en projektion en linjär avbildning P från ett vektorrum till sig själv sådant att P = P2 (man säger att P är idempotent).

En ortogonal projektion är inom linjär algebra en metod att bestämma en uppdelning av en vektor v i en del som ligger i ett underrum och den del som är ortogonal mot underrummet. Även ortogonala projektioner kan uttryckas som avbildningar, men framställas ofta som en formel, projektionsformeln.

Innehåll

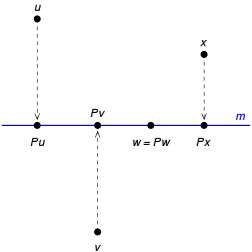
Ortogonala projektioner på vektorer och underrum

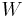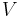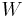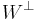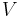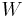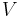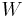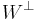Givet ett underrum W \, till det euklidiska rummet V \, så finns ett ortogonalt komplement till W \,, betecknat W^\perp , som består av alla vektorer i V \, som är ortogonala mot alla vektorer i W \,. Då kan en vektor v i V \, uttryckas som en summa av två vektorer i W \, respektive W^\perp :

v = v_{\| W} + v_{\perp W}, ~~ v_{\| W} \in W, ~~v_{\perp W} \in W^\perp

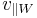v_{\| W} kallas den ortogonala projektionen på W.

Om f1,f2,..,fn är en ortogonal normerad bas i 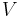V \, så ges en vektor v:s koordinater x1,x2,...xn i den basen genom skalärprodukten:

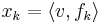x_k = \langle v, f_k \rangle .

Detta kommer av att varje vektor i 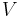V \, kan uttryckas som en linjärkombination av vektorer i en bas:

v = x_1f_1 + x_2f_2 + \dots + x_nf_n\,

om man applicerar en skalärprodukt på vektorn får man att:

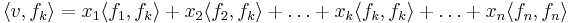\langle v, f_k \rangle = x_1\langle f_1, f_k \rangle + x_2\langle f_2, f_k \rangle + \dots + x_k\langle f_k, f_k \rangle + \dots + x_n\langle f_n, f_n \rangle.

Om basen är ortonomerad så kommer alla skalärprodukter där vänster- och högersidan är olika bli noll pga ortogonaliteten, och den skalärprodukt där vektorerna är lika bli ett pga normaliteten.

Av detta följer att om man vill veta projektionen av en vektor v på en annan vektor u (eller underrummet som spänns upp av u) som är normerad ges detta helt enkelt av:

v_{\| u} = \langle v, u \rangle

Om u inte är normerad blir inte 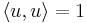\langle u, u \rangle = 1, och därför måste man kompensera:

v_{\| u} = \frac{\langle v, u \rangle}{\langle u, u \rangle} = \frac{\langle v, u \rangle}{|u|^2}

Om man har ett hyperplan π med normalvektorn n och vill projicera vektorn v på π kan detta göras med:

v_{\| \pi} = v - \frac{\langle v, n \rangle}{\langle n, n \rangle}

Då n spänner upp det ortogonala komplementet till π.

Detta kan generaliseras; om ett underrrum har flera normaler projicerar men helt enkelt på alla av dessa, alternativt projicerar man på basvektorerna för underrummet. Projektioner används i Gram-Schmidts ortogonaliseringsprocess.

Projektionsavbildningar

En avbildning P som uppfyller P = P2 kallas för en projektion.

Exempel

Avbildningen P projicerar punkterna ortogonalt på linjen m

Följande matris projicerar en vektor i 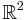\mathbb{R}^2 på y-axeln:

P = \begin{pmatrix} 0 & 0 \\ 0 & 1 \end{pmatrix}

Man ser här att om vektorn som P appliceras på inte har någon utsträckning x-led kommer den att bli oförändrad.

Följande matris projicerar en vektor i 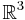\mathbb{R}^3 på xy-planet:

P = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{pmatrix}

Betrakta nu en godtycklig vektor:

v = \begin{pmatrix} x \\ y \\ z \end{pmatrix}

Och jämför Pv med P2v:

Pv = \begin{pmatrix} x \\ y \\ 0 \end{pmatrix}
P^2v = P\begin{pmatrix} x \\ y \\ 0 \end{pmatrix} = \begin{pmatrix} x \\ y \\ 0 \end{pmatrix}

Dvs, P = P2. Då P är en matris detta också ses genom direkt beräkning av P2 = P * P med matrismultiplikation.

Egenskaper

Projektioner på vektorrum har följande egenskaper:

  • Har endast egenvärdena 1 och 0
  • Determinanten till en projektion är noll, projektioner är därför inte inverterbara. Detta kan ses genom att använda faktumet att determinanten till en matris är produkten av egenvärdena. Om minst ett egenvärde är noll blir determinanten noll.

Ortogonala projektioner

Om vektorrummet som projektionen verkar i har en inre produkt, kan man prata om ortogonala projektioner. En ortogonal projketion har ett värderum som är ortogonalt mot dess nollrum. En projektion P är ortogonal om och endast om P = PT om vektorrummet är reellt (om vektorrummet är komplext så är kravet P = PH, där PH är P:s hermiteska konjugat). Antag att P = PT och betrakta vektorn x i vektorrummet. Ur projektionsdefinitionen kommer då att vektorn Px ligger då i P:s värderum och x − Px i P:s nollrum. För att två vektorer ska vara ortogonala ska skalärprodukten 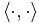\langle\cdot ,\cdot \rangle av de två vara noll:

\langle Px , x - Px \rangle= (Px)^T(x-Px) = x^T P^T(x-Px) = x^T (P - P^2)x = 0\,

Vilket visar att nollrummet är ortogonalt mot värderummet.

Hämtad från "https://sv.rilpedia.org/wiki/Projektion_(matematik)"
Personliga verktyg