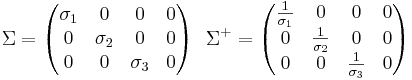Från Rilpedia

Moore-Penrose pseudoinvers är inom linjär algebra en generalisering av vissa egenskaper hos matrisinversen för icke-kvadratiska matriser, uppkallad efter Eliakim Hastings Moore och Roger Penrose, som beskrev den oberoende av varandra 1920 respektive 1955.

Innehåll 1 Definition 2 Egenskaper 3 Specialfall 3.1 Ortonormala rader och kolonner 3.2 Linjärt oberoende kolonner och rader 4 Beräkning 4.1 Singulärvärdesfaktorisering 5 Tillämpningar

Definition

Moore-Penrose pseudovinvers till en matris A är en matris A ⁺ som uppfyller:

1. AA ⁺ A = A       (AA ⁺ behöver inte vara en enhetsmatris, men ska avbilda alla kolonnvektorer i A på sig själva);
2. A ⁺ AA ⁺ = A ⁺       (A ⁺ is är en svag invers för den mulitplikativa semigruppen);
3. (AA ⁺ ) ^* = AA ⁺       (AA ⁺ är en hermitesk matris)
4. (A ⁺ A) ^* = A ⁺ A       (A ⁺ A är också hermitesk).

A ^* är det hermiteska konjugatet till A. För reella matriser är detta samma sak som transponatet.

Egenskaper

Givet en matris A med Moore-Penrose pseudoinvers A ⁺ , gäller följande:

• A ⁺ är unik.
• Om A är en inverterbar matris, är A ^{− 1} = A ⁺ .
• A ⁺ är sin egen invers, (A ⁺ ) ⁺ = A.
• AA ⁺ är en ortogonal projektion på As värderum.
• A ⁺ A är en ortogonal projektion på A ^* s värderum.
• Pseudoinversen till en nollmatris är dess transponat.

Specialfall

Ortonormala rader och kolonner

Om A har ortonormala kolonnvektorer (AA ^* = I) eller ortonormala radvektorer (A ^* A = I så är A ⁺ = A ^* .

Linjärt oberoende kolonner och rader

Om kolonnerna i A är linjärt oberoende är A ^* A inverterbar och Moore-Penrose pseudoinvers kan beräknas med:

A ⁺ = (A ^* A) ^{− 1}A ^* .

Det följer då att A ⁺ är vänsterinvers till A.

Om raderna i A är linjärt oberoende är AA ^* inverterbar och Moore-Penrose pseudoinvers kan beräknas med:

A ⁺ = A ^* (AA ^* ) ^{− 1}.

Det följer då att A ⁺ är högerinvers till A.

Beräkning

Singulärvärdesfaktorisering

Om matrisen A har singulärvärdesfaktoriseringen A = UΣV ^* så fås A ⁺ = VΣ ⁺ U ^* . Pseudoinversen av Σ, som är en "nästan diagonal" matris med matrisens singulärvärden i diagonalen, genom att ersätta varje element σ_i i diagonalen med 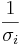. Exempel:

Tillämpningar

Moore-Penrose pseudoinvers ger en minsta kvadrat-lösning till system av linjära ekvationer. Om systemet ges av Ax = b ges minsta kvadrat-lösningen av x = A ⁺ b.