Lavalmunstycke

Från Rilpedia

Hoppa till: navigering, sök

Texten från svenska Wikipedia

Skiss på ett Lavalmunstycke. Visar ungefär hur flödeshastigheten ökar från grönt till rött i flödesriktningen

.

Ett lavalmunstycke är ett rör som är ihopknipt på mitten i timglasform. Det används för att accelerera gasflöden som förflyttar sig genom det i supersonisk fart. Det har stor användning i vissa typer av ångturbiner och moderna raketmotorer och supersoniska jet motorer. Analoga strömningsegenskaper har även funnit tillämpningar vid studiet av jetströmmar inom astrofysiken^[1].

Munstycket utvecklades på 1800-talet av den svenske uppfinnaren Gustaf de Laval. Lavalmunstycket påminner om ett venturirör och bådas fysikaliska egenskaper bestäms av Bernoullis ekvation. Dess funktion vilar på strömmande gasers olika egenskaper vid subsoniska och supersoniska hastigheter.

Innehåll

1 Fysikalisk princip
- 1.1 Matematisk härledning
- 1.2 Gasutflöden
2 Astronomisk tillämpning
3 Se även
4 Referenser

Fysikalisk princip

Eftersom hastigheten hos ett subsoniskt gasflöde tilltar om röret som det rör sig i smalnar av, därför att massflödet är konstant (gram per sekund). Gasflödet genom ett lavalmunstycke är isentropiskt (gasens entropi är konstant). Vid subsoniskt flöde är gasen kompressibel. Ljud, en liten longitudinell tryckvåg, kan röra sig genom den. Nära munstyckets midja, där tvärsnittsarean är minimum, blir gashastigheten lokalt transsonisk (Machtal = 1.0), ett villkor som kallas strypt flöde. När munstyckets tvärsnittsarea vidgas, fortsätter gasen att expandera och gasflödet ökar till supersonisk fart, där en ljudvåg inte kan röra sig tillbaka genom gasen sett i munstyckets viloreferensram (Machtal > 1.0).

Matematisk härledning

Ljudhastigheten c är en av ett mediums täthet $ρ$ avhängig storhet. Vad som machtalet M uttrycker, är just förhållandet mellan ett mediums strömningshastighet u och dess ljudhastighet c:

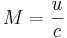$M = \frac{u}{c}$ (1)

Eulers rörelseekvationer ger tillsammans med tillståndsekvationen $d p / d ρ = c 2$ :

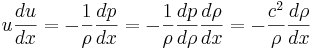$u \frac{du}{dx} = - \frac{1}{\rho} \frac{dp}{dx} = - \frac{1}{\rho} \frac{dp}{d\rho} \frac{d\rho}{dx} = - \frac{c^2}{\rho} \frac{d\rho}{dx}$ ,

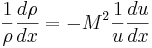$\frac{1}{\rho} \frac{d\rho}{dx} = -M^2 \frac{1}{u} \frac{du}{dx}$ , (2)

där $ρ$ är mediets täthet och $x$ är strömningsriktningen.

Ekvation (2) uttrycker att den relativa täthetsförändingen är proportionell mot den relativa hastighetsförändringen längs strömlinjerna, där proportionalitetsfaktorn är $M 2$ . Ur den kvadratiska proportionalitetsfaktorn följer att vid en underljudsströmning (M<1) så är den relativa täthetsförändingen väsentligt mindre än den relativa hastighetsförändringen. Omvänt är vid en överljudsströmning (M>1) den relativa täthetsförändingen väsentligt större än den relativa hastighetsförändringen.

Dessutom måste även kontinuitetsekvationen beaktas:

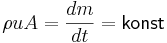$\rho u A = \frac{dm}{dt} = \mathsf{konst}$ ,

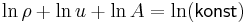$\ln \rho + \ln u + \ln A = \ln(\mathsf{konst})$ ,

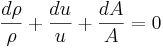$\frac{d\rho}{\rho} + \frac{du}{u} + \frac{dA}{A} = 0$ .

Differentierar man detta längs strömlinjen, så blir resultatet

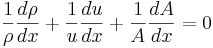$\frac{1}{\rho} \frac{d\rho}{dx} + \frac{1}{u} \frac{du}{dx} + \frac{1}{A} \frac{dA}{dx} = 0$ .

Med hänsyn till (2) följer ur detta

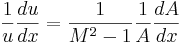$\frac{1}{u} \frac{du}{dx} = \frac{1}{M^2 - 1} \frac{1}{A} \frac{dA}{dx}$ . (3)

Tar man tvärsnsnittsarean A(x) för given, med u(x) och M(x) som obekanta, så gör uttrycket (3) en kvalitativ diskussion möjlig om flödet i ett munstycke. Önskar man påskynda flödet, alltså du/dx > 0, så följer ur (3):

vid underljudsströmning (M < 1), att dA/dx < 0 alltid gäller, så måste även munstycket smalna av,
vid överljudsströmning (M > 1), att dA/dx > 0 alltid gäller, så måste också munstycket vidga sig
vid soniskt flöde (M = 1) måste dysan ha ett konstant tvärsnitt.

Därur följer med tvingande nödvändighet lavalmunstyckets principiella form. I den konvergerande delen påskyndas det subsoniska flödet. Vid det trängsta tvärsnittet når det ljudhastighet. I den divergerande delen påskyndas slutligen flödet ytterligare till överljudsfart.

Gasutflöden

Avgasers linjära utloppshastighet kan med något utförligare härledning ^[2] ^[3] ^[4] beräknas med följande ekvation (ideal gas förutsatt):

$u_e = \sqrt{\;\frac{T\;R}{m}\cdot\frac{2\;k}{k-1}\cdot\bigg[ 1-(P_e/P)^{(k-1)/k}\bigg]}$

där:
u_e	= utloppshastighet vid munstyckets ände, m/s
T	= inloppsgasens absoluta temperatur, K
R	= Allmänna gaskonstanten = 8314,5 J/(kmol·K)
m	= gasens molekylmassa, kg/kmol (tidigare molekylvikt)
k	= c_p/c_v = isentropisk expansionsfaktor
c_p	= gasens specifika värme vid konstant tryck
c_v	= gasens specifika värme vid konstant volym
P_e	= utloppsgasens absoluta tryck vid munstyckets ände, Pa
P	= absolut tryck för inloppsgas, Pa

Avgasernas utgångshastighet u_e för raketmotorer ligger typiskt mellan 1,7 och 4,5 km/s beroende på drivmedlet.

Astronomisk tillämpning

Astrofysikerna har funnit att rör med lavalmunstyckets strömningsegenskaper har analoga fenomen i det interstellära mediet. De smala jetstrålar som sprutar ut från centrum på vissa radiogalaxer är ofta högst supersoniska. Det förefaller som om ett hett plasma, vilket på något sätt alstras av motormekanismen i aktiva galaxkärnor, skulle ha förkärlek till att smita ut i vinkelrät riktning från de gasskivor som observerats i värd-galaxernas centra. En sådan gasskiva skulle kunna ha samma funktion som röret i ingenjörstillämpningen, men med den skillnaden att dess inre inte längre är en solid vägg utan själv är en fluid, som kan innesluta jeten genom att tillhandahålla ett tryckbalanserat gränsskikt.

Samma tolkning har man gjort vid studiet av mer detaljerade bilder som tagits med rymdteleskopet Hubble av relativt närbelägna jets från några unga stjärnor. Naturens egna jetdysor åstadkommer dock dessutom fenomen som avviker från idealiserade steady-state lösningar. Även om termisk acceleration genom tryckgradienter uppträder, så får man räkna med att andra processer också spelar in, inte minst genom att magnetiska fält deltar i acceleration och kollimation av radio jets.

Se även

Referenser

↑ Cathy J. Clarke & Bob Carswell; Principles of Astrophysical Fluid Dynamics, kapitel 9, Cambridge University Press (2007). ISBN 978-0521853316
↑ Richard Nakka's ekvation 12
↑ Robert Braeuning's ekvation 2.22
↑ Sutton, George P.; Rocket Propulsion Elements: An Introduction to the Engineering of Rockets, 6e uppl. Sid 636, Wiley-Interscience (1992). 0471529389

[0] Cathy J. Clarke & Bob Carswell; Principles of Astrophysical Fluid Dynamics, kapitel 9, Cambridge University Press (2007). ISBN 978-0521853316

[1] Richard Nakka's ekvation 12

[2] Robert Braeuning's ekvation 2.22

[3] Sutton, George P.; Rocket Propulsion Elements: An Introduction to the Engineering of Rockets, 6e uppl. Sid 636, Wiley-Interscience (1992). 0471529389

[1]

[2]

[3]

[4]

Lavalmunstycke

Från Rilpedia

Innehåll

Fysikalisk princip

Matematisk härledning

Gasutflöden

Astronomisk tillämpning

Se även

Referenser

Visningar

Personliga verktyg

Sök

Navigering

Bibeln

Övrigt

Verktygslåda

På andra språk