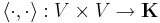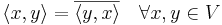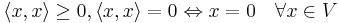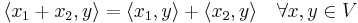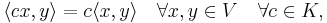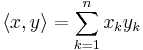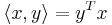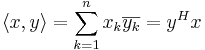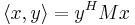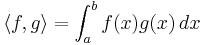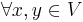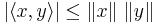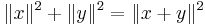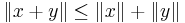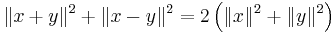Inre produktrum

Från Rilpedia

Texten från svenska Wikipedia

Inom matematiken är ett inre produktrum ett vektorrum med ytterligare struktur; en inre produkt (kallas också skalärprodukt) är definierad, vilket gör det möjligt att införa geometriska begrepp såsom vinklar och längden på vektorer.

Innehåll

1 Definition
2 Exempel
3 Egenskaper
4 Baser i inre produktrum
5 Se även

Definition

Låt V vara ett vektorrum över en kropp K. K kommer i fortsättningen antingen vara 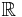$\mathbb{R}$ eller $\mathbb{C}$ . V är nu ett inre produktrum om det finns en funktion

$\langle \cdot, \cdot \rangle : V \times V \rightarrow \mathbf{K}$

som är

symmetrisk med undantag för komplexkonjugering

$\langle x, y \rangle = \overline{\langle y, x \rangle} \quad \forall x,y \in V$

detta innebär till exempel att 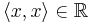$\langle x, x \rangle \in \mathbb{R}$

positivt definit:

$\langle x, x\rangle \geq 0, \langle x, x\rangle = 0 \Leftrightarrow x = 0 \quad \forall x \in V$

eftersom 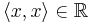$\langle x, x \rangle \in \mathbb{R}$ är detta väldefinierat.

linjär:

$\langle x_1 + x_2, y \rangle = \langle x_1, y \rangle + \langle x_2, y \rangle \quad \forall x,y \in V$

och

$\langle cx, y \rangle = c\langle x, y \rangle \quad \forall x,y \in V \quad \forall c \in K,$

Notera att denna definition för komplexa vektorrum innebär att den inre produkten är linjär i första variabeln, men antilinjär i den andra. Detta kallas ofta seskvilinjäritet. Detta är enbart en konvention, den inre produkten kan även definieras så att det omvända gäller. Oftast brukar man i matematiska sammanhang kräva linjäritet i första variabeln, medan man inom kvantfysik ofta vill ha linjäriteten i den andra variabeln.

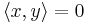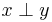Om $\langle x, y \rangle = 0$ sägs x och y vara ortogonala. Detta betecknas ofta som $x \perp y$ .

Exempel

Reella rum

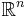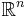I det ändligtdimensionella rummet $\mathbb{R}^n$ bestående av alla reella $n$ -tipler kan man införa den vanliga skalärprodukten som inre produkt, så om $x, y$ är element i $\mathbb{R}^n$ :

$\langle x, y \rangle = \sum_{k=1}^n x_ky_k$

Eller, uttryckt som matrismultiplikation:

$\langle x, y \rangle = y^Tx$

Där $y T$ är $y$ transponerat.

Komplexa rum

Om $n$ -tiplarna istället är komplexa så ges en inre produkt av:

$\langle x, y \rangle = \sum_{k=1}^n x_k \overline{y_k} = y^Hx$

Där $y H$ är det hermiteska konjugatet av $y$ och 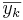$\overline{y_k}$ är det komplexa konjugatet av $y k$ .

En allmänare form för en inre produkt för 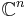$\mathbb{C}^n$ är:

$\langle x, y \rangle = y^HMx$

Där $M$ är en positivt definit matris. Detta gäller även för reella rum, då det hermiteska konjugatet blir transponat.

Funktionsrum

Det oändlighetsdimensionella funktionsrummet $C [a, b]$ av alla reella funktioner som är kontinuerliga på intervallet $[a, b]$ har en inre produkt:

$\langle f, g \rangle = \int_a^b f(x)g(x) \, d x$

Då $f, g \in C[a, b]$ .

Egenskaper

Det är lätt att visa att funktionen 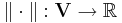$\| \cdot \|: \mathbf{V} \rightarrow \mathbb{R}$ sådan att 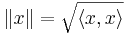$\|x\| = \sqrt{\langle x, x\rangle}$ är en norm på V. Om 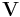$\mathbf{V}$ är fullständigt med avseende på metriken som ges av denna norm, kallas 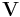$\mathbf{V}$ för ett Hilbertrum.

För ett inre produktrum gäller följande välkända satser:

Cauchy-Schwarz olikhet: $\forall x,y \in V$

$|\langle x, y \rangle| \leq \|x\| \ \|y\|$

Likhet gäller om och endast om x och y är linjärt beroende.

Pythagoras sats: om 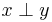$x \perp y$ så gäller

$\|x\|^2 + \|y\|^2 = \|x + y\|^2 \,$

Triangelolikheten: $\forall x,y \in V$

$\|x + y\| \leq \|x\| + \|y\|$

Lihet gäller om och endast om Cauchy-Schwarz olikhet är en likhet.

Parallellogramlagen: $\forall x,y \in V$

$\|x + y\|^2 + \|x - y\|^2 = 2\left(\|x\|^2 + \|y\|^2\right)$

Baser i inre produktrum

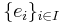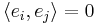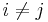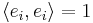En bas $\{e_i\}_{i \in I}$ för ett inre produktrum sägs vara en ortonormal bas (eller ON-bas; även termen ortogonal bas kan förekomma i denna mening) om det för alla element i basen gäller att $\langle e_i, e_j\rangle = 0$ om $i \neq j$ och $\langle e_i, e_i\rangle = 1$ för alla i. Givet en bas för ett ändligtdimensionellt inre produktrum 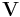$\mathbf{V}$ kan en ortonormal bas fås genom Gram-Schmidts ortogonaliseringsprocess.