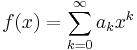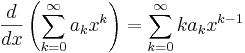Abels sats

Från Rilpedia

Texten från svenska Wikipedia

Abels sats eller Abels kriterium är en matematisk sats inom den matematiska analysen uppkallad efter Niels Henrik Abel. Satsen ger villkor för att en oändlig serie ska konvergera och finns i två utföranden, en för reella serier och en för potensserier inom komplex analys.

Historik

När Abel skrev sina första arbeten om algebraiska ekvationer så använde han oändliga serier utan att ta hänsyn till seriernas konvergens vilket var standard för matematiker verksamma under 1700-talet.

Dock när han senare arbetade med expansioner av elliptiska funktioner så behandlade han problemet mycket mer noggrannt. Han hade då uppmärksammat hur märkligt divergenta serier kan bete sig och att det inte fanns några bra bevis för när en serie konvergerar och när den divergerar.

Den 16 januari 1826 skrev Abel detta brev till sin före detta lärare Professor B. M. Holmboe angående divergenta serier "På det hela taget är divergenta serier djävulens verk och det är skamfullt att man vågar demonstrera något med hjälp av dem. Du kan få vilket resultat du vill när du använder dem, och de har gett upphov till så många katastrofer och så många paradoxer".

Som ett exempel på egendomliga egenskaper hos de divergenta serierna kan den divergenta serien $1 - 1 + 1 - 1...$ nämnas som beroende på hur man arrangerar termerna ger både gränsvärdet $(1 - 1) + (1 - 1) + (1 - 1) + ... = 0$ eller $1 - (1 - 1) - (1 - 1) + ... = 1$

Det faktum att det saknades bra bevis för konvergens och att både taylor- och binomialutveckling är serieutvecklingar innebar att Abel ansåg att de inte var tillräckligt välgrundade, varav han för binomialutvecklingen även producerade ett rigoröst bevis. Han började nu att angripa konvergensproblemet och kom slutligen fram med en sats i två utföranden.

Reell analys

Inom reell analys säger Abels sats att om $(a n)$ och $(b n)$ är talföljder av reella tal som uppfyller följande:

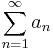$\sum_{n=1}^\infty a_n$ konvergerar

$(b_n)\,$ är monoton

$\lim_{n \to \infty} b_n \neq \pm \infty$ .

så kommer serien

$\sum_{n=1}^\infty a_n b_n.$

att konvergera.

Komplex analys

Den andra varianten av Abels sats ger tillräckliga villkor för att en potensserie ska konvergera på randen av sin konvergensskiva.

Om $(a n)$ är en monotont avtagande talföljd av positiva reella tal och:

$\lim_{n \to \infty} a_n = 0$

$\sum_{n=1}^\infty a_n z^n$ har konvergensradie 1, dvs serien konvergerar för alla $| z | < 1$ och divergerar för alla $| z | > 1$ ,

Då säger abels sats att serien konvergerar för hela enhetscirkeln $| z | = 1$ , förutom då $z = 1$ . Satsen kan inte användas för fallet $z = 1$ som därför måste undersökas separat.

Abels kriterium kan även appliceras på potensserier med konvergensradie $R \neq 1$ genom ett variabelbyte $w = z / R$ .

Abels sats bidrag till matematiken

Att veta när en serie konvergerar eller divergerar har en direkt nytta vid derivering och integrering av potensserier, ty om en funktion är given som en potensserie

$f(x)=\sum _{k=0} ^\infty a_k x^k$

kan den nämligen för $x$ innanför konvergensradien enkelt termvis deriveras enligt

$\frac{d}{dx} \left( \sum _{k=0} ^\infty a_k x^k \right) = \sum_{k=0} ^\infty k a_k x^{k-1}$

och integreras enligt

$\int \left( \sum _{k=0} ^\infty a_k x^k \right) dx = \sum _{k=0} ^\infty \frac{a_{k} x^{k+1} }{k+1}+C$ .

När Abel tog fram sina satser använde han sig av Abeltransformationer av serier vilket gav honom verktygen att bevisa kontinuiteten av potensseriernas summa fram till gränsvärdet då serien konvergerar, detta är även basen till en metod för att summera divergenta serier.

Abels sats

Från Rilpedia

Innehåll

Historik

Reell analys

Komplex analys

Abels sats bidrag till matematiken

Visningar

Personliga verktyg

Sök

Navigering

Bibeln

Övrigt

Verktygslåda

På andra språk