Tillståndsmaskin
Från Rilpedia
En Tillståndsmaskin (eng State Machine eller Automaton) är en abstrakt modell som används bland annat till att beskriva beteenden i mjukvara, inom hårdvarudesign, beräkningsteori och språkvetenskap. Användningsområdena är många, men generellt kan man säga att tillståndsmaskiner används för att beskriva skeenden i olika former med hjälp av tillstånd och villkor för övergång från ett tillstånd till ett annat.
Normalt ser man begreppet Tillståndsmaskin såsom synonymt med ändlig tillståndsmaskin (eng Finite State Machine eller Finite Automaton) eftersom en tillståndsmaskin måste ha ett ändligt antal tillstånd för att vara praktiskt användbar.
Innehåll |
Informell beskrivning
En typisk tillståndsmaskin består av ett antal tillstånd och ett antal övergångar mellan dessa tillstånd. Ett exempel på en tillståndsmaskin kan vara en modell för en dörr:
Modell för Dörr Tillstånd: Öppen eller Stängd Övergångar: Öppna eller Stäng
Man säger att en tillståndsmaskin alltid befinner sig i ett tillstånd, och om ett visst villkor uppfylls så övergår tillståndsmaskinen till ett annat tillstånd. Om till exempel tillståndsmaskinen för Dörr ovan befinner sig i tillståndet Stängd och någonting får villkoret för övergången Öppna att inträffa (dvs, någon öppnar dörren) så övergår tillståndsmaskinen till tillståndet Öppen.
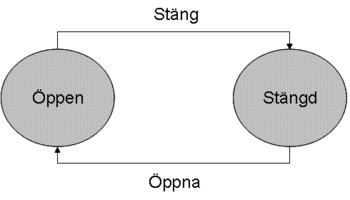
Man illustrerar oftast tillståndsmaskiner med bubblor som representerar tillstånd och pilar som representerar övergångar. Man skriver då villkoret för övergången vid pilen:
Vi inser här att vissa övergångar bara är meningsfulla för vissa tillstånd. Vi inser också att vi lätt kan införa tillståndet Låst till modellen för dörr.
När man arbetar med tillståndsmaskiner uppstår ofta delikata frågor. Man kan till exempel fråga sig om det ska finnas en övergång till Låst när dörren är i tillståndet Öppen. I praktiken är det ju möjligt att låsa en öppen dörr, men logiskt sett är det kanske inte meningsfullt.
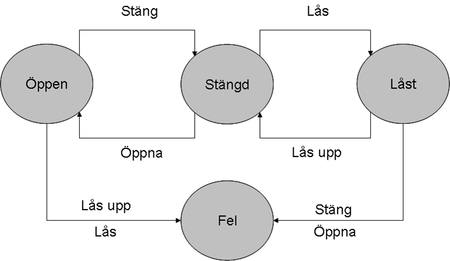
Ovan ser vi en bild av en utökad tillståndsmaskin för Dörr där tillstånden Låst och Fel har införts. Denna tillståndsmaskin är inte speciellt förlåtande, då dörren fastnar i tillståndet Fel om man antingen försöker låsa eller låsa upp den när den är öppen, eller om man försöker öppna eller stänga den när den är låst. Det kanske finns ett bättre sätt att hantera mänskliga felbeteenden på?
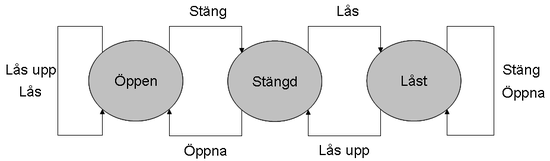
Här ser vi en mer förlåtande tillståndsmaskin för en dörr. En tillståndsmaskin som hanterar felbeteenden eller felaktig input förlåtande sägs vara robust.
Modellen för Dörr ser nu ut så här:
Modell för Dörr Tillstånd: Öppen, Stängd eller Låst Övergångar: Öppna, Stäng, Lås och Lås upp
Formell beskrivning
(Detta är en fri översättning av texten under Finite State Machine i engelska Wikipedia [1].)
En Finit Tillståndsmaskin (eng Finite State Machine (FSM) eller Finite Automaton) är ett mångsidigt och allmänt använt verktyg för att modellera beteenden med hjälp av tillstånd, övergångar och händelser.
- Ett tillstånd lagrar information om vad som har hänt under den tid som har gått sedan det system som tillståndsmaskinen modellerar startades - dvs, den reflekterar de stimuli som systemet har utsatts för från att det startades fram till nuet.
- En övergång indikerar en tillståndsändring, och den beskrivs av en händelse som måste inträffa för att övergången ska äga rum.
- En händelse är en beskrivning av en aktivitet som måste inträffa vid ett givet ögonblick.
Klassificering
Det går att särskilja två grupper av finita tillståndsmaskiner: Igenkänningsmaskiner och översättningsmaskiner.
Igenkänningsmaskiner
En igenkänningsmaskin matas med ett indata i någon form och meddelar sedan omvärlden om detta indata var korrekt eller ej enligt något kriterium. En igenkänningsmaskin används till exempel till att kontrollera att en sats skriven i ett formellt språk (se formell grammatik) är korrekt och välformad.
Översättningsmaskiner
Översättningsmaskiner används för att översätta ett indata från en symboluppsättning till en annan. Man kan särskilja två olika typer:
Moore-maskiner
En Moore-maskin använder endast ingångs-händelser. Detta innebär att när en tillståndsförändring inträffar i en Moore-maskin så produceras också en del av resultatet av systemets arbete i samband med övergången. Vilket resultat som produceras beror endast av vilket tillstånd som övergången sker till.
- Ett exempel: En hissdörr öppnas. Tillståndsmaskinen för hissdörrens beteende övergår från tillståndet Stängd till tillståndet Öppen. Samtidigt tänds belysningen inne i hissen
Mealy-maskiner
En Mealy-maskin använder endast indata-händelser. Detta innebär att när en tillståndsförändring inträffar i en Mealy-maskin så produceras också en del av resultatet av systemets arbete i samband med övergången. Vilket resultat som produceras beror, i motsats till Moore-maskinen, på vilket indata som ger upphov till övergången i kombination med vilket tillstånd som övergången sker till.
- Ett exempel: En hissdörr öppnas. Tillståndsmaskinen för hissdörrens beteende övergår från tillståndet Stängd till tillståndet Öppen. Samtidigt tänds belysningen inne i hissen om den öppnas manuellt. Om det är hissens egen dörrmotor som öppnar dörren tänds lampan inte
I praktiken används ofta en mix av dessa två maskintyper för översättning.
Deterministiska och icke-deterministiska finita tillståndsmaskiner
Man skiljer även mellan deterministiska och icke-deterministiska tillståndsmaskiner.
- En deterministisk finit tillståndsmaskin har exakt en definierad övergång för varje tillstånd för varje indata som är möjligt (korrekt) för detta tillstånd.
- För en icke-deterministisk finit tillståndsmaskin kan det finnas flera olika övergångar för ett givet tillstånd och ett givet korrekt ingångsdata.
Logiken bakom en Finit Tillståndsmaskin
Nästa tillstånd och utdata från en finit tillståndsmaskin är en funktion av det nuvarande indatat och tillståndet.
Matematisk modell
Det finns ett flertal definitioner av finita tillståndsmaskiner beroende på vilken typ man talar om
En igenkännarmaskin är en kvintupel (femställig symbolföljd) <Σ, S, s0, δ, F>, där:
- Σ är det som kallas maskinens indataalfabete (en ändlig icke-tom mängd av symboler)
- S är en ändlig icke-tom mängd av tillstånd
- s0 är det så kallade starttillståndet, ett element i S. Maskinen befinner sig alltså i tillståndet s0 när den startas.
- δ är tillståndsövergångsfunktionen: δ = S x Σ → S
- F är mängden av möjliga finaltillstånd, en (möjligen tom) [delmängd] av S
Även om en igenkännarmaskin saknar formell utdatafunktion (se nedan), så finns den där implicit - en boolesk funktion som returnerar Sant eller Falskt beroende på om indatat accepterades eller ej.
En översättarmaskin är en sextupel (sexställig symbolföljd) <Σ, Γ, S, s0, δ, ω>, där:
- Σ är det som kallas maskinens indataalfabete (en ändlig icke-tom mängd av symboler)
- Γ är det som kallas maskinens utdataalfabete (en ändlig icke-tom mängd av symboler)
- S är en ändlig icke-tom mängd av tillstånd
- s0 är det så kallade starttillståndet, ett element i S. Maskinen befinner sig alltså i tillståndet s0 när maskinen startas.
- δ är tillståndsövergångsfunktionen: δ: S x Σ → S
- ω är utdatafunktionen
Om utdatafunktionen är en funktion av ett tillstånd och av indataalfabetet (ω: S x Σ → Γ) är maskinen en Mealy-maskin.
Om utdatafunktionen enbart beror på ett tillstånd (ω: S → Γ) är maskinen en Moore-maskin.
Optimering
Att optimera en finit tillståndsmaskin innebär att man söker den maskin med minsta möjliga antal tillstånd som utför samma funktion. Detta kan utföras med så kallade färgläggningsalgoritmer.