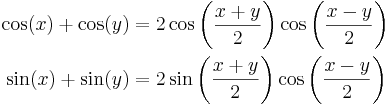Lista över trigonometriska identiteter

Från Rilpedia

(Omdirigerad från Sinus för dubbla vinkeln)

Hoppa till: navigering, sök

Texten från svenska Wikipedia

Följande är en lista över trigonometriska identiteter.

Innehåll

1 Grundläggande
2 Perioder
3 Symmetri
4 Förskjutningar
5 Trigonometriska ettan
6 Additions- och subtraktionsformler
7 Formler för dubbla vinkeln
8 Formler för tredubbla vinkeln
9 Formler för halva vinkeln
10 Formler för en produkt
11 Formler för en summa

Grundläggande

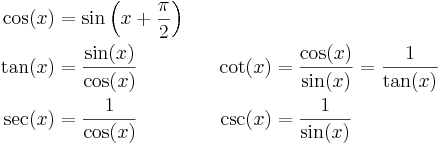
$\begin{align} \cos(x) &= \sin\left( x + \frac {\pi} {2}\right)\\ \tan(x) &= \frac{\sin(x)}{\cos(x)} &\quad \cot(x)&= \frac{\cos(x)}{\sin(x)} = \frac{1}{\tan(x)}\\ \sec(x) &= \frac{1}{\cos(x)} &\quad \csc(x)&= \frac{1}{\sin(x)} \end{align}$

Perioder

Sinus och cosinus har perioden 2π, tangens har perioden π. Om k är ett heltal gäller:

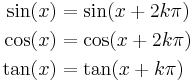
$\begin{align} \sin(x) &= \sin(x + 2k\pi) \\ \cos(x) &= \cos(x + 2k\pi) \\ \tan(x) &= \tan(x + k\pi) \\ \end{align}$

Symmetri

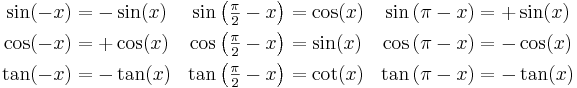
$\begin{align} \sin(-x) &= -\sin(x) & \sin\left(\tfrac{\pi}{2} - x\right) &= \cos(x) & \sin\left(\pi - x\right) &= +\sin(x) \\ \cos(-x) &= +\cos(x) & \cos\left(\tfrac{\pi}{2} - x\right) &= \sin(x) & \cos\left(\pi - x\right) &= -\cos(x) \\ \tan(-x) &= -\tan(x) & \tan\left(\tfrac{\pi}{2} - x\right) &= \cot(x) & \tan\left(\pi - x\right) &= -\tan(x) \\ \end{align}$

En funktion f(x) som uppfyller villkoret f(x) = f(-x) kallas jämn medan den kallas udda om det istället gäller att f(-x) = -f(x). Alltså är cosinusfunktionen jämn medan sinus- och tangensfunktionerna är udda.

Förskjutningar

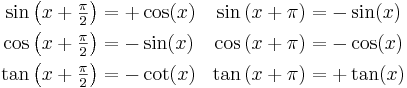
$\begin{align} \sin\left(x + \tfrac{\pi}{2}\right) &= +\cos(x) & \sin\left(x + \pi\right) &= -\sin(x) \\ \cos\left(x + \tfrac{\pi}{2}\right) &= -\sin(x) & \cos\left(x + \pi\right) &= -\cos(x) \\ \tan\left(x + \tfrac{\pi}{2}\right) &= -\cot(x) & \tan\left(x + \pi\right) &= +\tan(x) \\ \end{align}$

Trigonometriska ettan

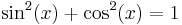
$\sin^2(x) + \cos^2(x) = 1\$

Additions- och subtraktionsformler

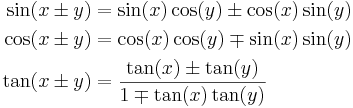
$\begin{align} \sin(x \pm y) &= \sin(x) \cos(y) \pm \cos(x) \sin(y) \\ \cos(x \pm y) &= \cos(x) \cos(y) \mp \sin(x) \sin(y) \\ \tan(x \pm y) &= \frac{\tan(x) \pm \tan(y)}{1 \mp \tan(x)\tan(y)} \\ \end{align}$

Formler för dubbla vinkeln

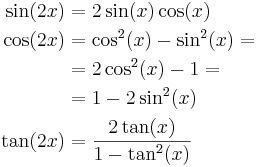
$\begin{align} \sin(2x) &= 2 \sin (x) \cos(x) \\ \cos(2x) &= \cos^2(x) - \sin^2(x) = \\ &= 2 \cos^2(x) - 1 = \\ &= 1 - 2 \sin^2(x) \\ \tan(2x) &= \frac{2 \tan (x)} {1 - \tan^2(x)} \\ \end{align}$

Formler för tredubbla vinkeln

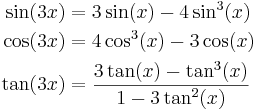
$\begin{align} \sin(3x) &= 3 \sin(x)- 4 \sin^3(x) \\ \cos(3x) &= 4 \cos^3(x) - 3 \cos(x) \\ \tan(3x) &= \frac{3 \tan(x) - \tan^3(x)}{1 - 3 \tan^2(x)} \end{align}$

Formler för halva vinkeln

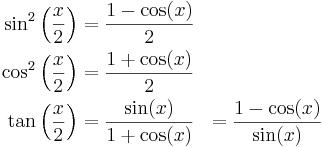
$\begin{align} \sin^2\left(\frac{x}{2}\right) &= \frac{1 - \cos(x)}{2} \\ \cos^2\left(\frac{x}{2}\right) &= \frac{1 + \cos(x)}{2} \\ \tan\left(\frac{x}{2}\right) &= \frac{\sin(x)}{1 + \cos(x)} &= \frac{1-\cos(x)}{\sin(x)} \end{align}$

Formler för en produkt

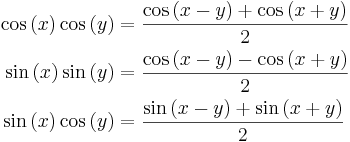
$\begin{align} \cos\left (x\right ) \cos\left (y\right ) &= {\cos\left (x - y\right ) + \cos\left (x + y\right ) \over 2} \\ \sin\left (x\right ) \sin\left (y\right ) &= {\cos\left (x - y\right ) - \cos\left (x + y\right ) \over 2} \\ \sin\left (x\right ) \cos\left (y\right ) &= {\sin\left (x - y\right ) + \sin\left (x + y\right ) \over 2} \\ \end{align}$

Formler för en summa

$\begin{align} \cos(x) + \cos(y) &= 2 \cos\left( \frac{x + y}{2} \right) \cos\left( \frac{x - y}{2} \right) \\ \sin(x) + \sin(y) &= 2 \sin\left( \frac{x + y}{2} \right) \cos\left( \frac{x - y}{2} \right) \\ \end{align}$