Stödvektormaskin
Från Rilpedia
En stödvektormaskin (eng. Support Vector Machine) är en typ av statistisk klassificerare, närmare bestämt en generaliserad linjär klassificerare. Den linjära formuleringen av algoritmen introducerades av Vladimir Vapnik 1963.
Metoden kan även användas för regression.
Stödvektormaskiner betraktas som robusta och har använts i många praktiska tillämpningar, till exempel för optisk teckenigenkänning samt ett stort antal olika områden inom språkteknologin och även objektigenkänning i datorseende. De kan hantera relativt stora träningsmängder och har metoder för att förhindra överanpassning.
Träning av stödvektormaskin
Antag att vi har en mängd exempel 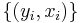 , där varje yi är ett klassvärde som är +1 eller -1, och varje xi är en attributvektor.
, där varje yi är ett klassvärde som är +1 eller -1, och varje xi är en attributvektor.
En stödvektormaskin med linjär kärna får vi då genom att finna det hyperplan (i det tvådimensionella fallet den linje) som maximalt separerar de två klasserna +1 och -1. Klassificeraren beskrivs då med hjälp av skalärprodukter med exempelvektorn och har den vanliga formen för en linjär klassificerare:
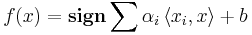
Ofta används inte den vanliga skalärprodukten (linjär kärna 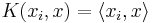 ) utan en skalärprodukt i ett högre rum (olinjär kärna
) utan en skalärprodukt i ett högre rum (olinjär kärna 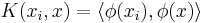 ). Då finns inte hyperplanet i attributrummet självt utan i ett rum av högre dimension (se generaliserad linjär klassificerare).
). Då finns inte hyperplanet i attributrummet självt utan i ett rum av högre dimension (se generaliserad linjär klassificerare).
Eftersom träningsdata ofta innehåller felaktigt klassificerade exempel ("brus") brukar man sätta en gräns C för hur stora konstanterna αi får bli, för att undvika överanpassning av klassificeraren.
För att finna hyperplanet löses ett kvadratiskt optimeringsproblem. Den vanligaste metoden att lösa optimeringsproblemet kallas SMO (sequential minimal optimisation) och är relativt enkel att implementera och snabb att lösa problemet.



