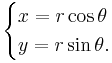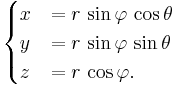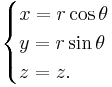Polära koordinater

Från Rilpedia

(Omdirigerad från Polära koordinatsystemet)
Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Polära koordinater är en form av koordinatsystem där en punkt identifieras av ett avstånd från en fix punkt plus en eller flera vinklar.


Innehåll

Tvådimensionella koordinatsystem

Cirkulära koordinater i ett plan (r,θ)

Cirkulära koordinater är ett annat namn för polära koordinater i två dimensioner. Här utgör avståndet r från origo O avståndskoordinaten, och vinkelkoordinaten bildas av vinkeln mellan en referenslinje (x-axeln) och linjen som går genom origo och punkten.

Formlerna för transformering från traditionella kartesiska koordinater till cirkulära koordinater då x≠0 är

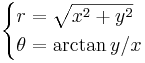\begin{cases} r = \sqrt{ x^2 + y^2} \\ \theta = \arctan{y/x} \end{cases}.

och formlerna för transformering från cirkulära koordinater till kartesiska är

\begin{cases}x = r\cos\theta \\ y = r\sin\theta .\end{cases}

Tredimensionella koordinatsystem

Sfäriska koordinater

sfäriska koordinater (r,θ,φ)

Sfäriska koordinater, eller rymdpolära koordinater består av två vinklar som anger en riktning och en radie som anger avstånd från origo.

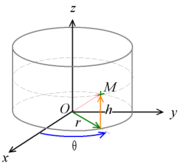
\begin{cases} x &= r \, \sin\varphi \, \cos\theta \\ y &= r \, \sin\varphi \, \sin\theta \\ z &= r \, \cos\varphi. \end{cases}

Cylindriska koordinater

cylindriska koordinater (r,θ,h)

Cylindriska koordinater (radie + vinkel + höjd) där de 2 första koordinterna är Cirkulära koordinater och den sista är punktens höjd över det plan de Cirkulära koordinaterna ligger i (ekvatorn), alltså

\begin{cases}x = r\cos\theta \\ y = r\sin\theta\\ z=z.\end{cases}

Hämtad från "https://sv.rilpedia.org/wiki/Pol%C3%A4ra_koordinater"
Personliga verktyg