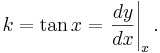Från Rilpedia

Inom matematiken är lutningen av eller riktningskoefficienten hos en rät linje (i Kartesiska koordinatsystemet) ett mått på hur brant linjen är (jämför tangent, sekant och derivata). Med algebraiska och geometriska argument kan lutningen för en rät linje beräknas; med analys kan lutningen för godtycklig funktionskurva beräknas.

Innehåll 1 Definition 2 Geometri 3 Algebra 4 Analys

Definition

Riktningskoefficienten för en rät linje (i det Kartesiska koordinatsystemet) ej parallell med y-axeln definieras som kvoten 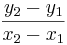där (x₁,y₁) och (x₂,y₂) är två olika punkter på linjen. Linjer parallella med y-axeln saknar riktningskoefficient.

Geometri

Ju större lutningen är desto brantare är kurvan. En horisontell linje har lutningen 0, en 45°-ig linje, som ligger högre åt höger, har lutningen +1, och en 45°-ig linje, som ligger lägre åt höger, har lutningen -1. Lutningen hos en strikt vertikal linje är inte ett reellt tal, men kan definieras som antingen -∞ eller +∞ i tillämpningar där detta är praktiskt.

Vinkeln θ mellan en linje och den positiva horisontella (x-)axeln (den sk riktningsvinkeln) är nära besläktad med lutningen m via tangentfunktionen

m = tan θ

och

θ = tan^-1 k

där tan^-1 = arctan.

Två linjer är parallella (||) i ett kartesiskt koordinatsystem om och endast om deras riktningskoeeficienter är lika stora - de är vinkelräta (⊥) (i ett ortonormerat koordinatsystem) om och endast om produkten av deras riktningskoefficienter är -1.

Algebra

Om ekvationen är given på formen

y = kx + m

så är lutningen koefficienten till variabeln x; som i detta fall k. Denna form av linjens ekvation kallas k-form, och m kan tolkas som y-värdet för linjens skärningspunkt med y-axeln.

Om lutningen k för en linje och en punkt (x₀, y₀) på linjen är kända kan linjens ekvation bestämmas med enpunktsformen

y - y₀ = k(x - x₀).

Enpunktsformeln är mer generell än k-formen, eftersom den är giltig även för vertikala linjer.

Analys

Inom analys kan man visa att lutningen är densamma som derivatan,