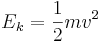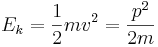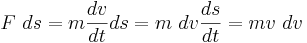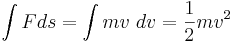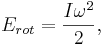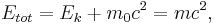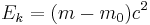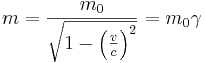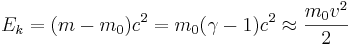Kinetisk energi

Från Rilpedia

(Omdirigerad från Levande kraft)

Hoppa till: navigering, sök

Texten från svenska Wikipedia

Kinetisk energi, eller rörelseenergi, för en kropp, är det mekaniska arbete som krävs för att reducera dess hastighet till noll.

Den kinetiska energin är

$E_k = {1\over 2}m v^2$

Då rörelsemängden är 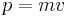$\ p = mv$ kan vi också skriva

$E_k = {1\over 2}m v^2 = {p^2 \over {2m}}$

Detta är ett resultat som gäller inom den klassiska mekaniken, det vill säga för hastigheter mycket mindre än ljusets hastighet.

Den totala kinetiska energin är bevarad i en elastisk stöt, ett specialfall av energiprincipen.

Innehåll

1 Kinetisk energi inom klassisk mekanik
- 1.1 Rotationsenergi
2 Kinetisk energi vid relativistiska hastigheter
3 Se även

Kinetisk energi inom klassisk mekanik

Giltigheten för den klassiska mekaniken omfattar de hastigheter som är avsevärt lägre än ljusets hastighet. Inom klassisk mekanik kan man beräkna rörelseenergin genom att ställa upp sambandet (kraften multiplicerad med vägen)

$F\ ds = m{dv\over dt}ds = m\ dv{ds \over dt} = mv\ dv$

och sedan beräkna integralen

$\int F ds = \int mv\ dv = {1\over 2}m v^2$

Detta är ett generellt resultat som gäller oberoende av den verkande kraftens natur.

Den uppmätta hastigheten för en kropp beror av den relativa rörelsen mellan observatören och kroppen. Rörelseenergin för en kropp är alltså beroende av den referensram i vilken hastigheten mäts.

Rotationsenergi

Den kinetiska energin för en roterande kropp med rotationshastigheten 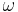$\ \omega$ , bestäms av sambandet

$E_{rot} = \frac{I\omega^2}{2},$

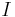där $\ I$ är kroppens tröghetsmoment.

Kinetisk energi vid relativistiska hastigheter

Detta avsnitt är en sammanfattning av Relativitetsteori

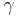Fil:Gamma.svg

$\ \gamma$ som funktion av v

För att bestämma den kinetiska energin för hastigheter nära ljusets hastighet, krävs ett relativistiskt samband för den totala energin:

$\ E_{tot} = E_k + m_0 c^2 = mc^2,$

det vill säga

$\ E_k = (m-m_0)c^2$

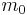där $\ m_0$ är vilomassan och den relativistiska massan är

$\ m = \frac{m_0}{{\sqrt{1-\left({v \over c}\right)^2}}} = m_0\gamma$

Genom till exempel taylorutveckling av 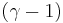$\ (\gamma - 1)$ och med antagandet att 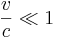${v \over c} \ll 1$ , går det att visa att formeln approximerar det klassiska uttrycket, det vill säga

$E_k = (m-m_0)c^2 = m_0(\gamma-1)c^2\approx\frac{m_0v^2}{2}$

Se även

Kinetisk energi

Från Rilpedia

Innehåll

Kinetisk energi inom klassisk mekanik

Rotationsenergi

Kinetisk energi vid relativistiska hastigheter

Se även

Visningar

Personliga verktyg

Sök

Navigering

Bibeln

Övrigt

Verktygslåda

På andra språk