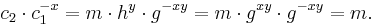ElGamal-kryptering
Från Rilpedia
ElGamal-kryptering är inom kryptografin ett system som baseras på asymmetrisk kryptering och Diffie-Hellmans nyckelöverenskommelse. Systemet uppfanns av Taher Elgamal 1984[1]. ElGamal används bl.a. av GNU Privacy Guard (GPG), nyare versioner av Pretty Good Privacy (PGP).
ElGamal-kryptering kan definieras med hjälp av en cyklisk grupp G. Krypteringens säkerhetsnivå beror på svårigheten på ett problem i G relaterat till beräkning av diskreta logaritmer.
Algoritmen
ElGamal-kryptering består av tre komponenter: nyckelgeneratorn, krypteringsalgoritmen och dekrypteringsalgoritmen.
Nyckelgeneratorn fungerar enligt följande, i en situation där Bob vill kunna ta emot krypterade meddelanden:
- Bob genererar en effektiv beskrivning av en cyklisk grupp G av ordning q och generator g.
- Bob tar ett slumpmässigt utvalt x från
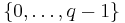 .
. - Bob beräknar
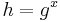 .
.
- Bob delar ut h tillsammans med beskrivningen av G,q,g som sin publika nyckel. Bob behåller x som sin privata nyckel, som hålls hemlig.
När Alice vill skicka ett hemligt meddelande M till Bob, krypterar hon det med hans publika nyckel (G,q,g,h), enligt krypteringsalgoritmen:
- Alice konverterar M till ett element m i G.
- Alice väljer ett slumpmässigt y ur
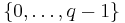 , och beräknar sedan
, och beräknar sedan
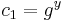 och
och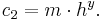
- Alice sänder chiffertexten (c1,c2) till Bob.
För att dekryptera chiffertexten (c1,c2) använder Bob sin privata nyckel x, enligt dekrypteringsalgoritmen:
- Bob beräknar
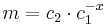 .
.
Detta fungerar eftersom
Om meddelandet M är för stort för G kan det delas upp i flera delar, där varje del kan krypteras individuellt.
Fotnoter
- ↑ Taher ElGamal, "A Public-Key Cryptosystem and a Signature Scheme Based on Discrete Logarithms", IEEE Transactions on Information Theory, v. IT-31, n. 4, 1985, pp469–472 or CRYPTO 84, pp10–18, Springer-Verlag.