Komplexitetsteori
Från Rilpedia
Komplexitetsteori är en sammanfattande benämning på den vetenskapsgren som behandlar system med följande egenskaper: de är komplexa (många obereonde enheter interagerar, t ex ett mänskligt samhälle eller den levande cellen); interaktionen inom systemet medför spontan självorganisering (t ex fåglar som anpassar sig till andra fåglar och därmed skapar en flock); de självorganiserande systemen är adaptiva (de försöker att vända händelser i dess omgivning till fördelar, tex en art utvecklas i riktning mot bättre anpassning till omgivningen eller företag som lär av erfarenheter); sådana komplexa, självorganiserande och adaptiva system har en dynamik som gör att de skiljer sig från statiska objekt som t ex datorer, som endast är komplicerade till skillnad från komplexa. Komplexa system är mer spontana, mer oordnade och mer levande - de befinner sig på randen till kaos, där systemen har tillräcklig stabilitet för att vara uthålliga, men samtidigt kan omvandlas. Randen till kaos är där komplexa system kan vara spontana, adaptiva, och levande.
Komplexitetsteori har sitt ursprung inom fysik, biologi, kemi och ekonomi och har nära kopplingar till kaosteori. Komplexitetsteori tillämpas inom forskning på vitt skilda områden, från organisation och kommunikation till datavetenskap och matematik.
Inom datavetenskapen handlar komplexitetsteori om att klassificera beräkningsproblem enligt hur väl algoritmer för att lösa dem kan prestera. Man talar bland annat om hur lång tid beräkningen kommer att ta, tidskomplexitet och hur mycket minne som kommer att behövas, minneskomplexitet alt. rumskomplexitet.
Ordobegreppet
Mängden data som algoritmen behandlar benämns n. Tidskomplexiteten för algoritmen är då det antal distinkta steg algoritmen kan behöva för att slutföra en beräkning, uttryckt som en funktion av datamängden n. Exempelvis, ett datorprogram som ska hitta platsen för ett visst element i en osorterad lista behöver i värsta fallet titta på varje element i listan. Ett sådant program får då tidskomplexiteten O(n), där O står för ordo. Ett program som tar konstant tid oavsett indatats storlek, exempelvis en uppslagning i en hashtabell, får O(1). Notera att tiden för varje steg i algoritmen i allmänhet är ointressant. Skulle man exempelvis komma fram till O(12n²) för en algoritm så anger man ändå bara O(n²). Detta eftersom skalfaktorn alltid blir insignifikant för tillräckligt stora värden på n, när man jämför algoritmer med olika komplexiteter.
På motsvarande sätt definieras minneskomplexitet, där det maximala använda minnet under algoritmens gång är det intressanta.
Formellt betyder 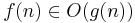 att det finns positiva konstanter N och c så att
att det finns positiva konstanter N och c så att 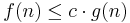 för alla n > N, vilket ska uttydas som att f(n) inte växer snabbare än g(n). Det är alltså inte det faktiska antalet steg i en algoritm man är ute efter (det är ofta starkt implementationsbundet) utan det asymptotiska uppträdandet: om datastorleken dubbleras, hur mycket mer tid kommer det då att ta? Om algoritmen är O(n) dubbleras även körtiden, men om algoritmen är O(n²) så kommer det att ta fyra gånger så lång tid.
för alla n > N, vilket ska uttydas som att f(n) inte växer snabbare än g(n). Det är alltså inte det faktiska antalet steg i en algoritm man är ute efter (det är ofta starkt implementationsbundet) utan det asymptotiska uppträdandet: om datastorleken dubbleras, hur mycket mer tid kommer det då att ta? Om algoritmen är O(n) dubbleras även körtiden, men om algoritmen är O(n²) så kommer det att ta fyra gånger så lång tid.
När man inom datalogin skriver O(g(n)) menar man egentligen Θ(g(n)). Det är nämligen fullt korrekt att säga att en O(n)-algoritm är av komplexiteten O(n2), vilket inte gäller för Θ.
| Notation | Definition |
|---|---|
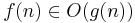 |
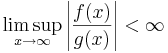 |
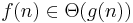 |
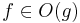 och och 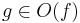 |
Komplexitetsklasser
Datalogiska problem kan delas upp i olika komplexitetklasser baserat på hur mycket resurser som behövs för att lösa det samt vilka operationer som är tillåtna.
Några viktiga komplexitetsklasser är P, som brukar representera problem där praktiskt tillämpbara algoritmer, och NP, där det endast är praktiskt möjligt att verifiera en lösning. Bokstaven P står för "polynomiell komplexitet" och ett beräkningsproblem ([beslutsproblem] om man ska vara noggrann) är i P om det finns en algoritm med en polynomiell värsta-fallet komplexitet, dvs den är O(nc) för nån konstant c. För NP, som står för non-deterministic polynomial time, alltså icke-deterministisk polynomiell tid, känner man bara till en algoritm som löser problemet i polynomiell tid om beräkningsmodellen är icke-deterministisk. Detta brukar uttryckas som att lösningar till problemet kan verifieras i polynomiell tid. Notera att 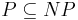 . Ett av den teoretiska datalogins stora olösta problem är om
. Ett av den teoretiska datalogins stora olösta problem är om 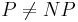 .
.
Ytterligare ett viktigt begrepp NP-fullständighet, ibland direktöversatt från engelskan till NP-komplett, som inbegriper dom i viss mening svåraste problemen i NP. Dessa har identifierats i förhoppning om att kunna avgöra om 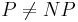 , men detta har hittills varit fruktlöst. Däremot har begreppet varit användbart för att identifiera problem som är i praktiken ogörliga att hantera på ett bra sätt när indata-storleken växer. Ett problem A är NP-fullständigt om det är i NP och man kan reducera varje annat problem i NP till A. Ett annat sätt att se det på är att säga att det är minst lika svårt som varje annat problem i NP.
, men detta har hittills varit fruktlöst. Däremot har begreppet varit användbart för att identifiera problem som är i praktiken ogörliga att hantera på ett bra sätt när indata-storleken växer. Ett problem A är NP-fullständigt om det är i NP och man kan reducera varje annat problem i NP till A. Ett annat sätt att se det på är att säga att det är minst lika svårt som varje annat problem i NP.
Undre gränser
Algoritmers komplexitet kan ses som övre gränser för hur svårt ett problem är. För att kunna avgöra om det finns ännu effektivare algoritmer för att problem kan det också vara intressant att reflektera över om det finns undre gränser för tidskomplexiteten. Med andra ord, finns det nån gräns för hur effektiva algoritmer man kan hitta för ett visst beräkningsproblem?
Här använder man sig av ett begrepp som är relaterat till ordo-begreppet. För två funktioner f och g gäller att 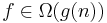 om
om 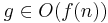 . Med hjälp av Ω säger man alltså att funktionen f växer minst lika snabbt som g.
. Med hjälp av Ω säger man alltså att funktionen f växer minst lika snabbt som g.
Det är ofta svårt att hitta undre gränser eftersom man på ett rigoröst matematiskt sätt måste visa att det verkligen inte finns någon algoritm som är mer effektiv. Det klassiska exemplet på en undre gräns gäller för sortering i en beräkningsmodell där man räknar antalet jämförelser. Då kan man visa att den undre gränsen är Ω(nlogn). Detta råkar matcha effektiviteten på flera sorteringsalgoritmer, som alltså är O(nlogn), och man kan därför säga att sorteringsproblemet är Θ(nlogn).



