Från Rilpedia

Sinusgång är det fenomen som kan uppstå när ett hjulpar på ett järnvägsfordon rullar längs spåret. Förutsättningen för att det ska uppstå är att hjulen har en konisk profil och att hjulen är förbundna med en stel axel.

Beskrivning

Eftersom hjulen är något koniska, kommer rullradien på höger och vänster sida att skilja sig åt då hjulparet inte rullar på centerlinjen. På grund av att hjulen måste ha samma rotationshastighet då de sitter ihop med axeln, kommer hjulparet sakta att gira. Girningen leder i sin tur att hjulparet inte rullar exakt rakt fram utan styr något i sidled. Detta får i sin tur i följd att hjulparet rör sig i sidled vartefter det rullar framåt längs spåret. Efter ett tag kommer hjulparet att vara förskjutet åt andra hållet, och processen upprepas. Hjulparet kommer under detta förlopp har beskrivit en rörelse som är sinusformad. Fenomenet kallas därför sinusgång. Se även rälsfordons gångegenskaper.

Analys

I analysen nedan görs antagandet om rullning utan glidning, rakt spår och små avvikelser från normalläget. Antag att hjulet är idealt koniskt (I verkligheten avviker vanliga hjulprofiler från en perfekt kon, men analysen blir liknande.). Låt konvinkeln vara γ och rullradien i kontaktpunkten vara r₀. Låt hjulparets förskjutning åt höger från mittlinjen vara y. Rullradien på höger sida kommer då att vara r₀ + tan(γ)y, och på vänster r₀ − tan(γ)y. Låt rotationshastigheten på axeln vara ω = v / r₀ där v är hjulaxelns hastighet framåt. Hastigheten på höger sida är då ω(r₀ + tan(γ)y) och vänster sida ω(r₀ − tan(γ)y).

Hastighetsskillnaden mellan höger och vänster sida är alltså ω2tan(γ)y. Denna kommer att ge upphov till en girhastighet på 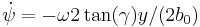där 2b₀ är nominella löpcirkelavståndet (1.5 m för normalspårvidd). Ytterligare samband är att girvinkeln är dy / dx = ψ och sambandet mellan derivator i tid och läge 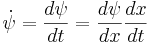. Med 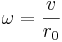fås genom att kombinera sambanden

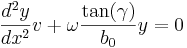
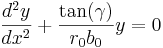
Detta är en differentialekvation, som har lösningen

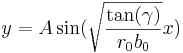
Sidorörelsen beskrivs alltså av en sinusfunktion, därav namnet på fenomenet. Sambandet mellan koniciteten γ och frekvensen (våglängden) är 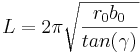Detta samband kallas Klingels formel.

Normalt är inte hjulprofilerna koniska utan profilens vinkel varierar med var på löpbanan man befinner sig. För sådana hjul talar man inte om konicitet utan om ekvivalent konicitet. Koniciteten för ett hjulpar med koniska profiler är lika med profilernas konvinkel.

Definition på ekvivalent konicitet: Antag ett hjulpar (i kombination med två rälprofiler) med godtyckliga hjulprofiler vars laterala rörelse har samma kinematiska våglängd som ett hjulpar med koniska profiler (på rakspår och i stora kurvradier). Den ekvivalenta koniciteten för hjulparet med godtyckliga profiler är samma som konvinkeln för hjulparet med koniska profiler.