Prims algoritm
Från Rilpedia
Prims algoritm är en girig algoritm för att skapa ett minimalt uppspännande träd från en godtycklig sammanhängande, viktad och oriktad graf.
Algoritmen finner i varje iteration den kant med lägst vikt som kan förbinda trädet med ett hörn som ännu inte finns med i trädet, varpå trädet utökas med denna kant (och det hörn som den ansluter till). Iterationen fortsätter så länge det finns hörn som inte lagts till i trädet.
Innehåll |
Pseudokod
algoritm PRIM
indata: graf, en sammanhängande, viktad och oriktad graf
rot, ett hörn i graf
resultat: Varje hörn i graf märks med sin förälder i ett minimalt
uppspännande träd av graf med det angivna hörnet som rot
samt med vikten av kanten till föräldern.
för varje hörn i graf
hörn.vikt ← ∞
hörn.förälder ← ogiltig
rot.vikt ← 0
kö ← en prioritetskö bestående av alla hörn i graf,
med minsta vikt som prioriteringsvärde
medan kö inte är tom
u ← extrahera_minsta( kö )
för varje hörn v som u ansluter till via en kant (u, v)
om v finns i kö och vikten av kanten (u, v) < v.vikt
v.förälder ← u
v.vikt ← vikten av kanten (u, v)
Exempel
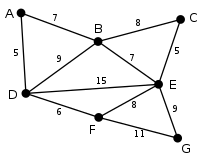
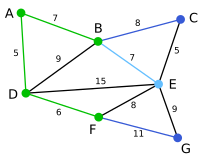
Målet är att finna ett träd som omfattar hörnen A–G där trädets kanter har så låg sammanlagd kostnad som möjligt. Algoritmen börjar vid hörn A.
Hörn D har kostnad 5, vilket är lägre än hörn B:s 7, och därför läggs hörn D till trädet.
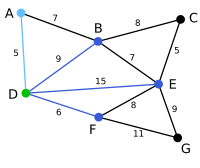
Hörn F ansluts, eftersom kostnaden för detta är 6, vilket är lägre än 7 (AB), 9 (DB) och 15 (DE).
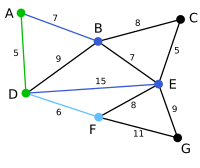
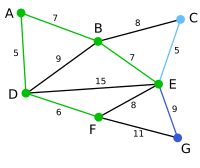
Hörn B ansluts via A. Kanten BD kommer inte att ingå i trädet, eftersom B och D redan är förbundna indirekt.
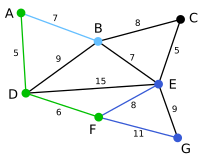
E ansluts via B.
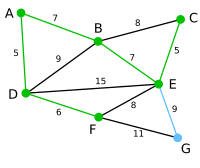
C ansluts via E.
G ansluts via E. Det finns inga fler hörn att ansluta. Trädet är fullständigt.
Tidskomplexitet
Prims algoritm har komplexitet O(E + V lg V), där E är antalet kanter och V är antalet hörn i den graf som trädet skapas från, under förutsättning att prioritetskön implementeras som en Fibonacciheap. (Om en binär heap används försämras komplexiteten till O(E lg V), vilket är asymptotiskt likvärdigt med Kruskals algoritm.)[1]
Se även
Referenser
- ↑ Cormen, T.H., Leiserson, E.L., Rivest, R.L., Stein, C: Introductions to Algorithms, MIT Press, USA 2001, 2 utgåvan, sid. 570–573. ISBN 0-262-03293-7.