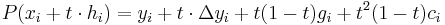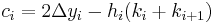Hermiteinterpolation
Från Rilpedia
Hermiteinterpolation, uppkallad efter franske 1800-talsmatematikern Charles Hermite, är en interpolationsmetod där man utgår från ett antal givna punkter och lutningen i dessa punkter för att beräkna punkter mellan de givna punkterna.
Metoden innebär att man beräknar nya punkter med hjälp av styckvisa tredjegradspolynom mellan varje par av punkter.
Om de givna punkterna betecknas (xi,yi) och lutningen i dessa punkter betecknas ki, bestäms punkter på det styckvisa tredjegradspolynomet P(x) genom Hermites interpolationsformel:
där
och
Formeln är en explicit algoritm så inga okända koefficienter behöver bestämmas.