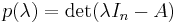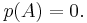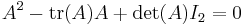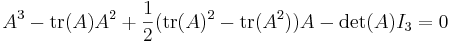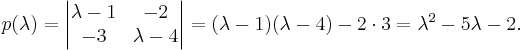Cayley-Hamiltons sats

Texten från svenska Wikipedia

Inom linjär algebra säger Cayley-Hamiltons sats (efter matematikerna Arthur Cayley och William Rowan Hamilton) att varje kvadratisk matris bestående av komplexa eller reella tal uppfyller sin egen karakteristiska ekvation.

Dvs: om $A$ är en given n×n matris och I_n är identitetsmatrisen med dimensionerna n×n, så definieras A:s karakteristiska ekvation som:

$p(\lambda)=\det(\lambda I_n-A)\,$

där "det" betecknar determinanten. Cayley-Hamiltons sats säger att om man ersätter $λ$ med $A$ i den karakteristiska ekvationen erhålls nollmatrisen:

$p(A)=0.\,$

Exempel

För tvådimensionella matriser fås

$A^2-\mbox{tr}(A)A+\det(A)I_2=0\,$

I tre dimensioner blir uttrycket

$A^3-\mbox{tr}(A)A^2+\frac{1}{2}\big(\mbox{tr}(A)^2-\mbox{tr}(A^2)\big)A-\det(A)I_3=0$

För att ta ett numeriskt lite tydligare exempel. Ta exempelvis matrisen

$A = \begin{bmatrix}1&2\\ 3&4\end{bmatrix}.$

Karakteristiska ekvationen ges av

$p(\lambda)=\begin{vmatrix}\lambda-1&-2\\ -3&\lambda-4\end{vmatrix}=(\lambda-1)(\lambda-4)-2\cdot3=\lambda^2-5\lambda-2.$

Cayley-Hamiltons sats säger att

A 2 - 5 A - 2 I 2 = 0

Vilket snabbt kan verifieras i det här fallet.

Ett resultat av detta är att Cayley-Hamiltons sats kan användas för att beräkna potenser av matriser på ett enklare sätt än att multiplikation.

Om vi tar resultatet ovan och sen skriver om lite får vi

A 2 - 5 A - 2 I 2 = 0

A 2 = 5 A + 2 I 2 .

Om vi sen vill beräkna exempelvis A⁴

A 3 = (5 A + 2 I 2) A = 5 A 2 + 2 A = 5(5 A + 2 I 2) + 2 A = 27 A + 10 I 2

A 4 = A 3 A = (27 A + 10 I 2) A = 27 A 2 + 10 A = 27(5 A + 2 I 2) + 10 A

A 4 = 145 A + 54 I 2 .