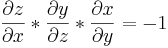Barkhausers rörformel

Från Rilpedia

Hoppa till: navigering, sök
Wikipedia_letter_w.pngTexten från svenska WikipediaWikipedialogo_12pt.gif
rpsv.header.diskuteraikon2.gif
icon_anmal.gif
rp-wp-sv.gif

Barkhausers rörformel härledes från början från elektrotekniken där den användes vid beräkningar av elektronrör. Dess tillämpningsområde är i dagsläget mestadels inom termodynamiken.

Låt F(x,y,z) vara en en funktion av klass C1 från R3 till R

Antag att F:s partiella derivator är skilda från noll i punkten (a,b,c)

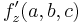f^\prime_z (a,b,c) ≠ 0

Detta medför (enligt implicita funktionssatsen) att i en omgivning av (a,b,c) är z en partiellt deriverbar funktion av x och z med

{\partial z \over \partial x} = -{\partial f'_x \over \partial f'_z}

På Samma sätt leder 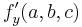f^\prime_y (a,b,c) ≠ 0 till att y är

{\partial y \over \partial z} = -{\partial f'_z \over \partial f'_y}

Av f^\prime_x (a,b,c) ≠ 0 får vi

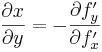
{\partial x \over \partial y} = -{\partial f'_y \over \partial f'_x}

Från dessa får vi Barkhausers rörformel

{\partial z \over \partial x} * {\partial y \over \partial z} * {\partial x \over \partial y} = -1


Se även

Elektronrör

Hämtad från "https://sv.rilpedia.org/wiki/Barkhausers_r%C3%B6rformel"
Personliga verktyg