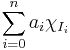Stegfunktion

Från Rilpedia

Texten från svenska Wikipedia

En stegfunktion eller trappfunktion är en styckvis konstant funktion. I definitionen nedan är ser man att stegfunktioner kan uttryckas som ändliga linjärkombinationer av mycket enkla funktioner.

Trappfunktioner används vid definitionen av Riemannintegralen.

Definition

En funktion $f (x)$ är en stegfunktion om det finns reella tal $x 0, x 1,..., x n,α 1,...,α n$ och funktioner $p 1 (x), p 2 (x),..., p n (x)$ sådana att

$x 0 < x 1 < ... < x n$
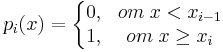
$p_i(x) = \left\{\begin{matrix} 0, & om \;x<x_{i-1} \\ 1, & om \;x\geq x_i \end{matrix}\right.$
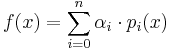
$f(x) = \sum_{i=0}^n \alpha_i \cdot p_i(x)$

Detta kan även formuleras som att $f (x)$ kan skrivas

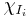$\sum_{i=0}^n a_i\chi_{I_i}$

där $\chi_{I_i}$ där är indikatorfunktionen för intervallet $I i$ .

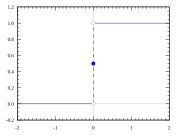
Enhetsstegfunktionen

Heavisides stegfunktion.

Ett exempel på en stegfunktion är enhetsstegfunktionen eller Heavisides stegfunktion. Det är den funktion $u (x)$ (även betecknad $θ(x)$ ) som antar värdet 0 då $x < 0$ och värdet 1 då $x > 0$ (vad den antar för värde i $x = 0$ är oftast oväsentligt och definieras därmed endast om så behövs).

Se även

Enkel funktion

Denna matematik-relaterade artikel är bara påbörjad. Du kan hjälpa till genom att utöka den.

Stegfunktion

Från Rilpedia

Definition

Enhetsstegfunktionen

Se även

Visningar

Personliga verktyg

Sök

Navigering

Bibeln

Övrigt

Verktygslåda

På andra språk