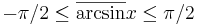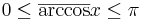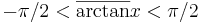Principalvärde
Från Rilpedia
| Artikeln eller avsnittet innehåller ifrågasatta faktauppgifter. Se diskussionssidan, eller historiken, för mer information. Rätta gärna felaktigheter. |
Principalvärde har med de cykliska funktionerna att göra.
De cykliska funktionerna är tänkta att vara inversa funktioner till de trigonometriska funktionerna, men eftersom dessa är periodiska är de inte omvändbara.
För att komma tillrätta med detta, väljer man ett principalvärde inom ett visst intervall, som ska vara det värde som tilldelas den cykliska funktionen.
För att bli mer konkret:
På moderna funktionsräknedosor och grafiska räknedosor finns funktioner som betecknas t ex sin-1 placerade på samma tangemt som sin etc. Eftersom (sin 30°=) sin(π / 6) blir 0,5 ger sin-1 0,5 svaret 30 (om räknedosan är inställd på grader) eller 0,5235987755 dvs π / 6 om dosan är inställd på radianer.
Men ekvationen
- sin x = 0,5
har lösningarna
- x1 = π / 6 + 2πn
- x2 = 5π / 6 + 2πn
dvs oändligt många värden.
Av dessa väljer man ut ett värde (i princip det som räknedosan svarar med) och kallar det för principalvärdet av arcsin och skriver 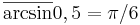
Märk särskilt att räknedosans beteckningar är olämpliga.
Värdemängderna för principalvärdena för de viktigaste cykliska funktionerna är