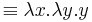Lambdakalkyl
Från Rilpedia
Lambdakalkyl (λ-kalkyl) är i ett formellt system som skapades för att undersöka funktioner och rekursion. Lambdakalkylen utvecklades på 1920-talet av Alonzo Church. På 1960-talet förstod man att lambdakalkylen kunde användas för att förstå programspråk.
Det har därför blivit den matematiska grunden för funktionella programspråk.
Objekten i lambdakalkyl är termer (som ibland kallas lambdatermer). Det finns tre typer av termer
- Variabler, x, y, z, ...
- abstraktion, λx.t där t är en term
- applikation,
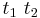 där t1 och t2 är termer
där t1 och t2 är termer
Abstraktion kan ses som definition av en funktion och applikation motsvarar tillämpning av en funktion.
På termerna använder man olika typer av reduktioner för att visa satser om lambdakalkylen. Lite förenklat är reduktionerna:
- α-reduktion - namnen på variblerna kan bytas
- β-reduktion - en term
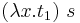 reduceras till termen t2 som är termen t1 med alla x utbytta mot s
reduceras till termen t2 som är termen t1 med alla x utbytta mot s - η-konvertering - termen
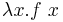 konverteras till termen f
konverteras till termen f
Churchkodning
För att använda lambdakalkyl för programspråk behöves bland annat tal och booleska värden. De finns inte i lambdakalkylen men de kan kodas med så kallad Churchkodning.
Booleska värden
- true
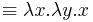
- false